SCENARIO 12-11 a Computer Software Developer Would Like to UseANOVASimple Linear Regression 12-41 -Referring to Scenario 12-11, Which

The Answer of SCENARIO 12-11 a Computer Software Developer Would Like to UseANOVASimple Linear Regression 12-41 -Referring to Scenario 12-11, Which

SCENARIO 12-11 a Computer Software Developer Would Like to UseANOVASimple Linear Regression 12-41 -Referring to Scenario 12-11, Which

The Answer of SCENARIO 12-11 a Computer Software Developer Would Like to UseANOVASimple Linear Regression 12-41 -Referring to Scenario 12-11, Which

Solved

SCENARIO 12-11
a Computer Software Developer Would Like to Use

question 37

Short Answer

SCENARIO 12-11
A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware.Following is the output from a simple linear regression
along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed:
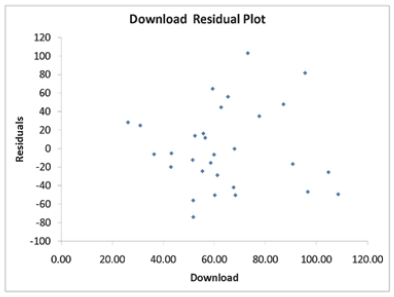$SCENARIO 12-11 A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \begin{array}{lr} \hline {\text { Regression Statistics }} \\ \hline \text { Multiple R } & 0.8691 \\ \text { R Square } & 0.7554 \\ \text { Adjusted R Square } & 0.7467 \\ \text { Standard Error } & 44.4765 \\ \text { Observations } & 30.0000 \\ \hline \end{array} ANOVA \begin{array}{llll} \hline & {\text { df }} & {\text { SS }} &{\text { MS }} & F & \text { Significance F } \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \text { Residual } & 28 & 55386.4309 & 1978.1582 & & \\ \text { Total } & 29 & 226451.3503 & & & \end{array} \begin{array}{lllll} \hline & \text { Coefficients } & \text { Standard Error } & \text { t Stat } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\ \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \\ \hline \end{array} Simple Linear Regression 12-41 -Referring to Scenario 12-11, which of the following is the correct alternative hypothesis for testing whether there is a linear relationship between revenue and the number of downloads? a) H _ { 1 } : b _ { 1 } = 0 b) H _ { 1 } : b _ { 1 } \neq 0 c) H _ { 1 } : \beta _ { 1 } = 0 d) H _ { 1 } : \beta _ { 1 } \neq 0$ $\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8691 \\ \text { R Square } & 0.7554 \\ \text { Adjusted R Square } & 0.7467 \\ \text { Standard Error } & 44.4765 \\ \text { Observations } & 30.0000 \\\hline\end{array}$

ANOVA
$\begin{array}{llll} \hline & {\text { df }} & {\text { SS }} &{\text { MS }} & F & \text { Significance F } \\\hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \text { Residual } & 28 & 55386.4309 & 1978.1582 & & \\ \text { Total } & 29 & 226451.3503 & & &\end{array}$

$\begin{array}{lllll}\hline & \text { Coefficients } & \text { Standard Error } & \text { t Stat } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\\text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \\\hline\end{array}$
$SCENARIO 12-11 A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \begin{array}{lr} \hline {\text { Regression Statistics }} \\ \hline \text { Multiple R } & 0.8691 \\ \text { R Square } & 0.7554 \\ \text { Adjusted R Square } & 0.7467 \\ \text { Standard Error } & 44.4765 \\ \text { Observations } & 30.0000 \\ \hline \end{array} ANOVA \begin{array}{llll} \hline & {\text { df }} & {\text { SS }} &{\text { MS }} & F & \text { Significance F } \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \text { Residual } & 28 & 55386.4309 & 1978.1582 & & \\ \text { Total } & 29 & 226451.3503 & & & \end{array} \begin{array}{lllll} \hline & \text { Coefficients } & \text { Standard Error } & \text { t Stat } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\ \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \\ \hline \end{array} Simple Linear Regression 12-41 -Referring to Scenario 12-11, which of the following is the correct alternative hypothesis for testing whether there is a linear relationship between revenue and the number of downloads? a) H _ { 1 } : b _ { 1 } = 0 b) H _ { 1 } : b _ { 1 } \neq 0 c) H _ { 1 } : \beta _ { 1 } = 0 d) H _ { 1 } : \beta _ { 1 } \neq 0$ Simple Linear Regression 12-41 $SCENARIO 12-11 A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \begin{array}{lr} \hline {\text { Regression Statistics }} \\ \hline \text { Multiple R } & 0.8691 \\ \text { R Square } & 0.7554 \\ \text { Adjusted R Square } & 0.7467 \\ \text { Standard Error } & 44.4765 \\ \text { Observations } & 30.0000 \\ \hline \end{array} ANOVA \begin{array}{llll} \hline & {\text { df }} & {\text { SS }} &{\text { MS }} & F & \text { Significance F } \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \text { Residual } & 28 & 55386.4309 & 1978.1582 & & \\ \text { Total } & 29 & 226451.3503 & & & \end{array} \begin{array}{lllll} \hline & \text { Coefficients } & \text { Standard Error } & \text { t Stat } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\ \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \\ \hline \end{array} Simple Linear Regression 12-41 -Referring to Scenario 12-11, which of the following is the correct alternative hypothesis for testing whether there is a linear relationship between revenue and the number of downloads? a) H _ { 1 } : b _ { 1 } = 0 b) H _ { 1 } : b _ { 1 } \neq 0 c) H _ { 1 } : \beta _ { 1 } = 0 d) H _ { 1 } : \beta _ { 1 } \neq 0$
-Referring to Scenario 12-11, which of the following is the correct alternative hypothesis for testing whether there is a linear relationship between revenue and the number of downloads? a) $H _ { 1 } : b _ { 1 } = 0$
b) $H _ { 1 } : b _ { 1 } \neq 0$
c) $H _ { 1 } : \beta _ { 1 } = 0$
d) $H _ { 1 } : \beta _ { 1 } \neq 0$

Distinguish between direct and indirect transmission of infectious diseases.

Articulate the role and function of the lymphatic system in disease defense.

Explain the mechanism and importance of vaccines in preventing infectious diseases.

Identify the major types of pathogens and their associated diseases.

Definitions:

Currency Exchange

The process by which one currency is converted into another, enabling international trade and investment.

Nationalizations

The process by which governments take private assets into public ownership, typically key industries or resources.

Polycentric

An approach in international business where a company gives autonomy to each host country operation to tailor strategies and practices to local conditions.

Geocentric

An approach or viewpoint that considers the earth as the center, often used in the context of international business to describe a strategy that views the world as a potential market with no inherent borders.