Solve the Problem Using Technology, Perform the Following Hypothesis Test: at the 5

question 46

Multiple Choice

Solve the problem. Use the critical-value approach.
-A machine that fills soda bottles is supposed to fill them to a mean volume of 16.2 fluid ounces. A random sample of 20 filled bottles produced the following volumes in fluid ounces: 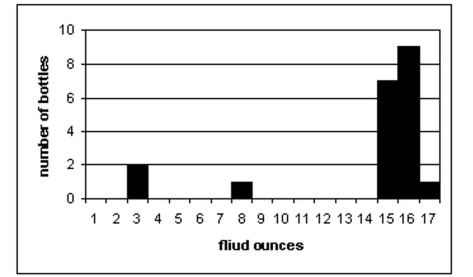$$\begin{array}{l}\begin{array} { l l l l l l l l l l } 16.3 & 15.9 & 16.7 & 15.3 & 17.1 & 16.4 & 3.9 & 15.9 & 16.2 & 3.4 \\16.4 & 8.2 & 15.5 & 16.5 & 16.0 & 16.3 & 15.8 & 16.7 & 16.5 & 15.5\end{array}\\\text { These data are summarized on the following histogram: }\end{array}$$

Using technology, perform the following hypothesis test: at the 5% significance level,determine Whether the fill volume is less than the supposed value. Comment on the appropriateness of the Test.

• A) Test statistic: \(t = - 1.8063\); Critical value: \(- 2.0921\). Since the test statistic is greater than the critical value, do not reject the null hypothesis \(\mathrm { H } _ { 0 } : \mu = 16.2 \mathrm { oz }\). There is insufficient evidence to conclude that the fill volume is below \(16.2\) oz. The conclusion is on sound statistical ground.
• B) Test statistic: \(t = - 1.8063\); Critical value: \(- 1.7254\). Since the test statistic is less than the critical value, do not reject the null hypothesis \(\mathrm { H } _ { 0 } : \mu =\) \(16.2 \mathrm { oz }\). There is insufficient evidence to conclude that the fill volume is below \(16.2\) oz. However, the data exhibits 3 outliers. Elimination of these outliers may alter the conclusion.
• C) Test statistic: \(t = - 1.8063\); Critical value; \(- 2.0921\). Since the test statistic is greater than the critical value, do not reject the null hypothesis \(\mathrm { H } _ { 0 } : \mu = 16.2 \mathrm { oz }\). There is insufficient evidence to conclude that the fill volume is below \(16.2\) oz. However, the data exhibits 3 outliers. Elimination of these outliers may alter the conclusion.
• D) Test statistic: \(t = - 1.8063\); Critical value: \(- 1.729\). Since the test statistic is less than the critical value, reject the null hypothesis \(\mathrm { H } _ { 0 } : \mu = 16.2 \mathrm { oz }\). There is sufficient evidence to conclude that the fill volume is below \(16.2 \mathrm { oz }\). However, the data exhibits 3 outliers. Elimination of these outliers may alter the conclusion.

---

Definitions:

Vertical Integration

A business strategy where a company controls multiple stages of production or distribution within the same industry.

Ethnic Group

A community of people who share common cultural characteristics, ancestry, or national origin.

Nerdy Students

Individuals who are highly enthusiastic or knowledgeable about academic, technical, or specialized subjects, often regarded as intellectually inclined or socially awkward.

Dragon Ladies

A stereotype referring to strong, domineering, or mysterious East Asian women, often portrayed in a negative or overly exoticized manner.