The Regression Below Predicts the Daily Number of Skiers Who $F$

question 12

Essay

The regression below predicts the daily number of skiers who visit a small ski resort based on three explanatory variables.
The data is a random sample of 30 days from the past two ski seasons. The variables are: SKIERS the number of skiers who visit the resort on that day
SNOW the number of inches of snow on the ground
TEMP the high temperature for the day in degrees $F$ .
WEEKDAY an indicator variable, weekday $= 1$ , weekend $= 0$
Dependent variable is Skiers
R squared $= 25.4 \% \quad \mathrm { R }$ squared (adjusted) $= 16.8 \%$
$s = 125.1$ with $30 - 4 = 26$ degrees of freedom



$\begin{array}{lrrrr}\text { Variable } & \text { Coefficient } & \text { SE(Coeff) } & \text { t-ratio } & \text { p-value } \\\text { Constant } & 559.869 & 76.78 & 7.29 & <0.0001 \\\text { Snow } & 1.424 & 2.70 & 0.53 & 0.6019 \\\text { Temp } & -1.604 & 2.77 & -0.58 & 0.5677 \\\text { Weekend } & 147.349 & 51.86 & 2.84 & 0.0086\end{array}$



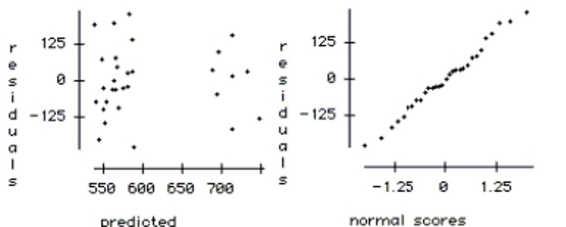
-If you think that the temperature might affect attendance differently on weekends than on
weekdays, how would you change the regression to test this?

---

Definitions:

Direct Materials

Raw materials that are directly traceable to the production of a specific good or service and are a significant portion of the production cost.

Standard Quantity

The expected amount of materials or inputs required to produce a unit of product under normal operating conditions.

Direct Materials Quantity Variance

The variance between the real amount of direct materials consumed during manufacturing and the anticipated standard amount.

Standard Materials Quantity

The expected amount of materials that should be used for the production of a certain number of units, as set by a company's standards.