The Regression Below Predicts the Daily Number of Skiers Who $F$

question 18

Essay

The regression below predicts the daily number of skiers who visit a small ski resort based on three explanatory variables.
The data is a random sample of 30 days from the past two ski seasons. The variables are: SKIERS the number of skiers who visit the resort on that day
SNOW the number of inches of snow on the ground
TEMP the high temperature for the day in degrees $F$ .
WEEKDAY an indicator variable, weekday $= 1$ , weekend $= 0$
Dependent variable is Skiers
R squared $= 25.4 \% \quad$ R squared (adjusted) $= 16.8 \%$
$\mathrm { s } = 125.1$ with $30 - 4 = 26$ degrees of freedom


$\begin{array} { l r r r r } \text { Variable } & \text { Coefficient } & \text { SE(Coeff) } & \text { t-ratio } & \text { p-value } \\ \text { Constant } & 559.869 & 76.78 & 7.29 & < 0.0001 \\ \text { Snow } & 1.424 & 2.70 & 0.53 & 0.6019 \\ \text { Temp } & - 1.604 & 2.77 & - 0.58 & 0.5677 \\ \text { Weekend } & 147.349 & 51.86 & 2.84 & 0.0086 \end{array}$


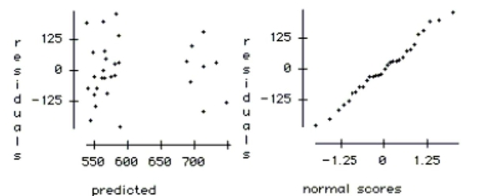
-Which of the explanatory variables appear to be associated with the number of skiers, and
which do not? Explain how you reached your conclusion.

---

Definitions:

Marketing Research

The process of gathering, analyzing, and interpreting data regarding market conditions, customer preferences, and competition to inform business decisions.

Marketing Program

A comprehensive plan that outlines the advertising, sales, and promotional activities for a product or service to reach its target market.

Marketing Mix

The set of controllable variables that a business uses to influence consumers' buying decisions, traditionally identified as product, price, place, and promotion.

Cool Mint Chocolate

A flavor profile combining the refreshing taste of mint with the rich, sweet taste of chocolate.