Here Are Data About the Average January Low Temperature in Cities

question 19

Essay

Here are data about the average January low temperature in cities in the United States, and factors that might allow us to
predict temperature. The data, available for 55 cities, include: We will attempt to make a regression model to help account for mean January temperature and to understand the effects of
the various predictors.
At each step of the analysis you may assume that things learned earlier in the process are known.
Units Note: The "degrees" of temperature, given here on the Fahrenheit scale, have only coincidental language relationship to
the "degrees" of longitude and latitude. The geographic "degrees" are based on modeling the Earth as a sphere and dividing it
up into 360 degrees for a full circle. Thus 180 degrees of longitude is halfway around the world from Greenwich, England
(0°) and Latitude increases from 0 degrees at the Equator to 90 degrees of (North) latitude at the North Pole.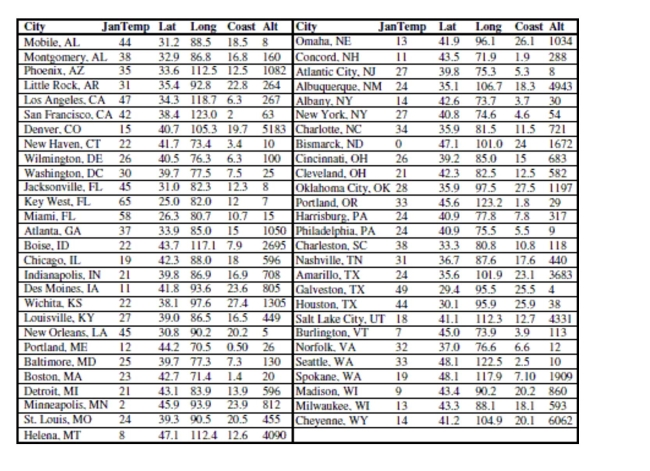
-Now, consider longitude. Should the longitude of a city have an influence on average
January low temperature? Here is the regression: Dependent variable is: JanTemp
R squared $= 0.1 \% \quad$ R squared (adjusted) $= - 1.8 \%$
$s = 13.61$ with $55 - 2 = 53$ degrees of freedom
$\begin{array} { l l l l l } \text { Source } & \text { Sum of Squares } & \text { df } & \text { Mean Square } & \text { F-ratio } \\ \text { Regression } & 8.34647 & 1 & 8.34647 & 0.045 \\ \text { Residual } & 9817.18 & 53 & 185.230 & \\ & & & & \\ \text { Variable } & \text { Coefficient } & \text { SE(Coeff) } & \text { t-ratio } & \text { P-value } \\ \text { Intercept } & 24.0487 & 11.40 & 2.11 & 0.0396 \\ \text { Long } & 0.026186 & 0.1234 & 0.212 & 0.8327 \end{array}$
Test the null hypothesis that the true coefficient of Long is zero in this regression. State the
null and alternative hypotheses and indicate your procedure and conclusion.

Identify and explain Jung's principles of psychic energy: principle of opposites, principle of equivalence, and principle of entropy.

Recognize how Jung's childhood experiences influenced his later theories and the development of analytical psychology.

Describe the concept of archetypes and their significance in Jung's theory of the collective unconscious.

Differentiate between Jung's and Freud's views on the unconscious and the role of dreams in their theories.

---

Definitions:

Susceptible

Likely or prone to be affected by a particular condition or occurrence.

Social Responsibility

The ethical theory that individuals and organizations are obligated to act for the benefit of society at large.

Volunteerism

The practice of offering one's time and services to community projects or organizations without financial compensation.

Adolescents

Young people in the transitional stage of physical and psychological development from childhood to adulthood, typically aged between 13 and 19.