Penicillin Doctors Studying How the Human Body Assimilates Medication Inject $= 90.8 \% \quad$

question 37

Essay

Penicillin Doctors studying how the human body assimilates medication inject some
patients with penicillin, and then monitor the concentration of the drug (in units/cc) in the
patients' blood for seven hours. The data are shown in the scatterplot. First they tried to fit
a linear model. The regression analysis and residuals plot are shown. Dependent variable is:
Concentration
No Selector
R squared $= 90.8 \% \quad$ R squared (adjusted) $= 90.6 \%$
$s = 3.472$ with $43 - 2 = 41$ degrees of freedom


$\begin{array}{llrrr}\text { Source } & \text { Sum of Squares } & \text { df } & \text { Mean Square } & \text { F-ratio } \\\text { Regression } & 4900.55 & 1 & 4900.55 & 407 \\\text { Residual } & 494.199 & 41 & 12.0536 &\end{array}$



$\begin{array}{lllrl}\text { Variable } & \text { Coefficient } & \text { s.e. of Coeff } & \text { t-ratio } & \text { prob } \\\text { Constant } & 40.3266 & 1.295 & 31.1 & \leq 0.0001 \\\text { Time } & -5.95956 & 0.2956 & -20.2 & \leq 0.0001\end{array}$




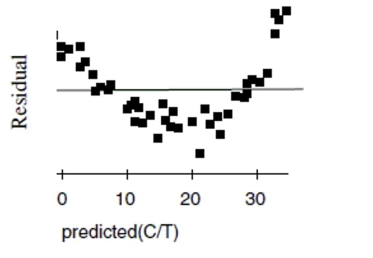
a. Find the correlation between time and concentration.
b. Using this model, estimate what the concentration of penicillin will be after 4 hours.
c. Is that estimate likely to be accurate, too low, or too high? Explain.
Now the researchers try a new model, using the re-expression log(Concentration). Examine
the regression analysis and the residuals plot below. Dependent variable is: LogCnn
No Selector
R squared $= 98.0 \% \quad$ R squared (adjusted) $= 98.0 \%$
$s = 0.0451$ with $43 - 2 = 41$ degrees of freedom


$\begin{array}{llrrr}\text { Source } & \text { Sum of Squares } & \text { df } & \text { Mean Square } & \text { F-ratio } \\\text { Regression } & 4.11395 & 1 & 4.11395 & 2022 \\\text { Residual } & 0.083412 & 41 & 0.002034 &\end{array}$

$\begin{array}{llllc}\text { Variable } & \text { Coefficient } & \text { s.e. of Coeff } & \text { t-ratio } & \text { prob } \\\text { Constant } & 1.80184 & 0.0168 & 107 & \leq 0.0001 \\\text { Time } & -0.172672 & 0.0038 & -45.0 & \leq 0.0001\end{array}$

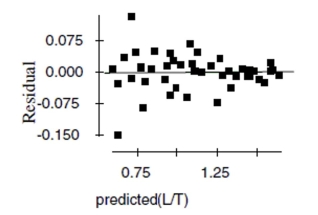
d. Explain why you think this model is better than the original linear model.
e. Using this new model, estimate the concentration of penicillin after 4 hours.