For Each Integer $n \geq 0$ , Let $P ( n )$

question 3

Essay

For each integer $n \geq 0$ , let $P ( n )$ be the equation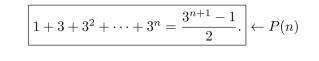

(Recall that by definition $1 + 3 + 3 ^ { 2 } + \cdots + 3 ^ { n } = \sum _ { i = 0 } ^ { n } 3 ^ { i }$ )
(a) Is P(0) true? Justify your answer.
(b) In the inductive step of a proof that $P ( n )$ is true for all integers $n \geq 0$ , we suppose $P ( k )$ is true (this is the inductive hypothesis), and then we show that $P ( k + 1 )$ is true. Fill in the blanks below to write what we suppose and what we must show for this particular equation.
Proof that for all integers $k \geq 0$ , if $P ( k )$ is true then $P ( k + 1 )$ is true:
Let $k$ be any integer that is greater than or equal to 3 , and suppose that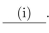
We must showthat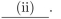
(c) Finish the proof started in (b) above.

---

Definitions:

Intelligence Tests

Standardized exams designed to measure human intelligence, aptitude, or cognitive abilities.

Creative Blocks

A condition where an individual is unable to access their creativity, leading to difficulty in producing new work.

Operant Conditioning

A method of learning that employs rewards and punishments for behavior.

Rational-emotive Therapy

A form of cognitive-behavioral therapy founded by Albert Ellis that helps individuals identify and change irrational beliefs that cause emotional distress.