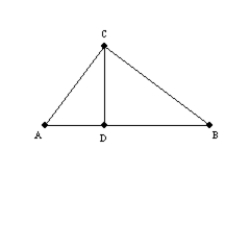
-Supply Missing Statements and Missing Reasons for the Proof of This

question 12

Essay

-Supply missing statements and missing reasons for the proof of this theorem.
"The altitude drawn to the hypotenuse of a right triangle separates the right triangle into two
right triangles that are similar to each other."
Given: Right triangle ABC with rt. ; 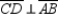Prove: 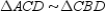S1. R1.
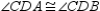S2. R2.
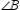S3. and are comp. R3. The acute angles of a rt. 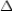are comp.
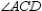S4. and are comp. R4.
S5. R5. If 2 s are comp. to the same , these are .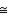
S6. R6.

---

Definitions:

Variable Costs

Costs that change in proportion to the level of goods or services a business produces or sale, such as materials and labor.

Sales

The total amount of goods or services sold by a company within a specific period, generating revenue.

Operating Leverage

A financial ratio that measures the degree to which a firm can increase operating income by increasing revenue, highlighting the fixed versus variable costs structure.

Financial Leverage

The use of borrowed funds to increase the potential return on investment, amplifying both potential gains and losses.