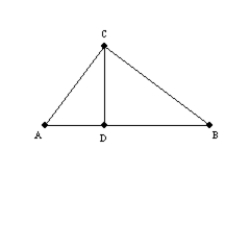
-Supply Missing Statements and Missing Reasons for the Proof of This

question 12

Essay

-Supply missing statements and missing reasons for the proof of this theorem.
"The altitude drawn to the hypotenuse of a right triangle separates the right triangle into two
right triangles that are similar to each other."
Given: Right triangle ABC with rt. ; 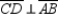Prove: 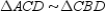S1. R1.
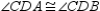S2. R2.
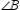S3. and are comp. R3. The acute angles of a rt. 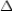are comp.
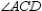S4. and are comp. R4.
S5. R5. If 2 s are comp. to the same , these are .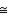
S6. R6.

---

Definitions:

AaMm

Represents a genotype consisting of two different alleles, Aa, for one trait and two different alleles, Mm, for another trait, indicating a hybrid individual.

Dominant Allele

An allele that expresses its phenotype even in the presence of a different (recessive) allele at the same genetic locus in a heterozygote.

Aniridia

A congenital condition characterized by the complete or partial absence of the iris, affecting the individual's vision.

Genotype AAbbCc

The genetic makeup of an organism consisting of two alleles for one trait, with one being dominant A, aa indicating recessive, and Bb Cc being heterozygous.