
-Supply missing statements and missing reasons for the following proof.
Given: 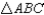 ;
; 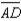 bisects
bisects 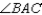 and
and 
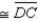 Prove:
Prove: 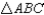 is an isosceles triangle
is an isosceles triangle
S1. 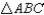 ;
; 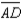 bisects
bisects 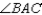 R1.
R1.
S2. 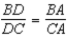 R2. If a ray bisects one
R2. If a ray bisects one 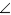 of a
of a  , it divides the opposite
, it divides the opposite
side into segments whose lengths are proportional to
the lengths of the two sides that form the bisected 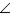 .
.
S3. R3. Given
S4. 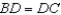 R4.
R4.
S5. 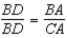 , so
, so 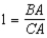 R5.
R5.
S6. 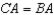 R6.
R6.
S7. R7.
Definitions:
Severe Depression
A psychiatric disorder identified by lasting feelings of despondency or a lack of enjoyment in hobbies, seriously affecting normal life.
Manic Episodes
Periods of abnormally elevated mood and high energy, often characteristic of bipolar disorder.
Negative Symptoms
Features primarily associated with schizophrenia and similar disorders, characterized by a lack or decrease in normal functions, such as motivation, emotional expression, or social engagement.
Social Withdrawal
The act of pulling away from others and choosing to spend time alone, avoiding social interactions.
Q4: The primary care pediatric nurse practitioner inserts
Q8: The primary care pediatric nurse practitioner is
Q10: Consider the drawing provided. Using the auxiliary
Q13: The parent of a toddler and a
Q122: Where <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt="Where ,
Q275: The line with equation y = mx
Q308: In kite WXYZ, WX = WZ and
Q411: The statement, "If 2 parallel lines are
Q627: Name the expression that completes this form
Q686: If the word MOM is relected across