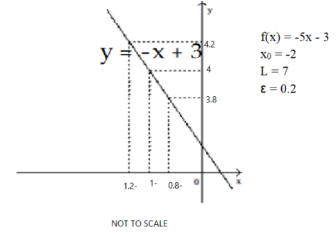
Find the Limit $L$ For the Given Function $f$ , the Point $x _ { 0 }$

question 48

Multiple Choice

Find the limit $L$ for the given function $f$ , the point $x _ { 0 }$ , and the positive number $\varepsilon$ . Then find a number $\delta > 0$ such that, for all $x _ { t } 0 < \left| x - x _ { 0 } \right| < \delta \Rightarrow | f ( x ) - L | < \varepsilon$ .
-

• A) 5
• B) 0.4
• C) 0.2
• D) -0.2

---

Definitions:

Third Market

Trading venue for exchange-listed stocks that occurs off the official exchange, often involving large institutional investors through over-the-counter (OTC) transactions.

Fourth Market

Trading of securities directly between investors, bypassing traditional brokerage and exchange platforms.

OTC Markets

Over-the-counter markets refer to decentralized markets where trading occurs directly between two parties without the supervision of an exchange.

Institution-To-Institution Trading

The buying and selling of securities between institutional investors, like pension funds and mutual funds, rather than individual investors.