SCENARIO 15-4 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing) , daily mean of the percentage of students attending class (% Attendance) , mean teacher salary in dollars (Salaries) , and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Let Y = % Passing as the dependent variable, 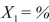 Attendance,
Attendance, 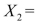 Salaries and
Salaries and  Spending. The coefficient of multiple determination (
Spending. The coefficient of multiple determination ( 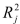 ) of each of the 3 predictors with all the other remaining predictors are, respectively, 0.0338, 0.4669, and 0.4743. The output from the best-subset regressions is given below:
) of each of the 3 predictors with all the other remaining predictors are, respectively, 0.0338, 0.4669, and 0.4743. The output from the best-subset regressions is given below:  Following is the residual plot for % Attendance:
Following is the residual plot for % Attendance: 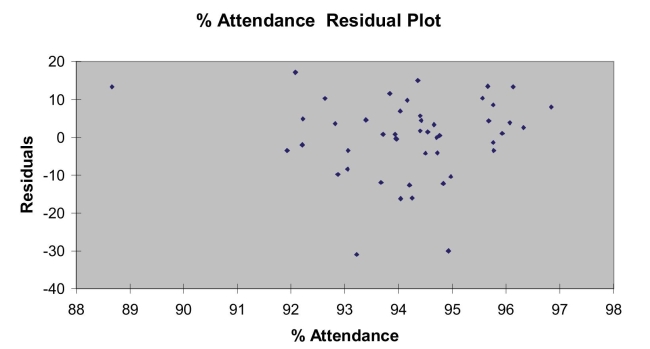 Following is the output of several multiple regression models:
Following is the output of several multiple regression models: 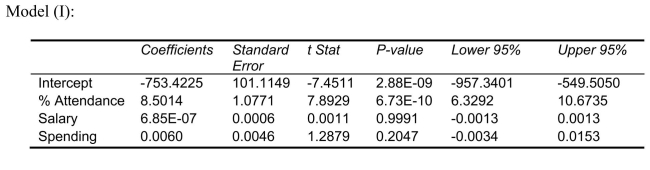

-Referring to Scenario 15-4, the "best" model chosen using the adjusted R-square statistic is
Definitions:
Commission Rates
The percentage or fixed fee that a salesperson receives as compensation for their sales contributions.
Sales Total
The aggregate amount from all sales transactions within a given period.
Account Receivable
Money owed to a business by its customers for goods or services that have been delivered but not yet paid for.
Outstanding Debt
The total amount of borrowed money that has not yet been repaid by the borrower.
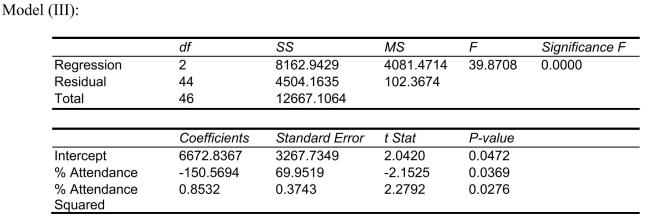
Q20: Referring to Scenario 15-4, the quadratic effect
Q27: Referring to Scenario 14-3, the p-value for
Q50: Referring to Scenario 15-6, what is the
Q102: Referring to Scenario 17-3, what is the
Q117: The principle of parsimony indicates that the
Q152: Referring to Scenario 16-9, if one decides
Q157: Referring to Scenario 16-11, using the second-order
Q158: Referring to Scenario 14-18, what are the
Q160: Referring to Scenario 18-8, which of the
Q186: Suppose the light bulbs in a factory