Solve the Problem. -The Quadratic Function 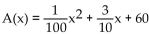Fits the Following Data. Use the Data

question 105

Multiple Choice

Solve the problem.
-The quadratic function fits the following data. Use the function to estimate the number of daytime accidents that occur at 60 km/h.

• A) 156 per 200,000,000 kilometers driven
• B) 114 per 200,000,000 kilometers driven
• C) 78.6 per 200,000,000 kilometers driven
• D) 54 per 200,000,000 kilometers driven

---

Definitions:

Competitive Advantage

The attribute that allows an organization to outperform its competitors, leading to greater sales or margins and/or retaining more customers.

Mass Production

A manufacturing process characterized by the high-volume production of standardized goods using assembly line techniques.

Assembly-Line System

An efficient manufacturing process where a product is assembled step by step in a sequential manner by workers stationed at fixed positions.

Uniform Products

Goods that are produced to be identical in quality and performance, ensuring consistency across all units.