Use This Information,along with Its Associated Sensitivity Report,to Answer the Following

question 19

Multiple Choice

Use this information,along with its associated Sensitivity Report,to answer the following questions.
A production manager wants to determine how many units of each product to produce weekly to maximize weekly profits.Production requirements for the products are shown in the following table.
$$\begin{array} { | c | c | c | c | } \hline \underline { \text { Product } } & \frac { \text { Material 1 } } { ( \mathrm { lbs } ) } & \frac { \text { Material 2 } } { ( \mathrm { lbs } . ) } & \text { Labor (hours) } \\\hline \underline { \underline { \mathrm { A } } } & \underline { 3 } & \underline { 2 } & \underline { 4 } \\\hline \underline { \mathrm { B } } & \underline { 1 } & \underline { 4 } & \underline { 2 } \\\hline \underline { \mathrm { C } } & \underline { 5 } & \underline { \text { none } } & \underline { 3.5 } \\\hline\end{array}$$
Material 1 costs $7 a pound,material 2 costs $5 a pound,and labor costs $15 per hour.Product A sells for $101 a unit,product B sells for $67 a unit,and product C sells for $97.50 a unit.Each week there are 300 pounds of material 1;400 pounds of material 2;and 200 hours of labor.The output of product A should not be more than one-half of the total number of units produced.Moreover,there is a standing order of 10 units of product C each week.
$$\begin{array}{l}\text { Formulation }\\\begin{array} { l l } \ { \text { Max } } & 10 \mathrm {~A} + 10 \mathrm {~B} + 10 \mathrm { C } \\\text { Subject to: } & \\& 3 \mathrm {~A} + \mathrm { B } + 5 \mathrm { C } \leq 300 \text { (constraint \#1) } \\& 2 \mathrm {~A} + 4 \mathrm {~B} \leq 400 \text { (constraint \#2) } \\& 4 \mathrm {~A} + 2 \mathrm {~B} + 3.5 \mathrm { C } \leq 200 \text { (constraint \#3) } \\& \mathrm { C } \geq 10 \text { (constraint \#4) } \\& \mathrm { A } , \mathrm { B } , \mathrm { C } \geq 0\end{array}\end{array}$$

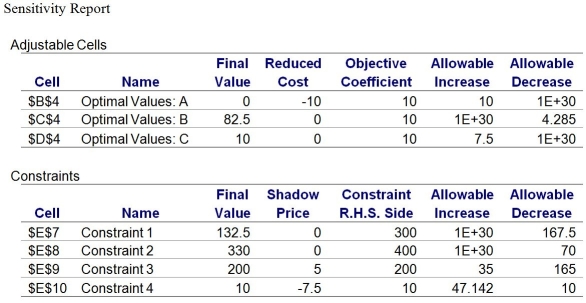
-What is the optimal objective function value?

Comprehend the role and necessity of blinding in experiments.

Identify different types of experimental designs.

Grasp the principles behind the use of incentives in experiments and their potential effects.

Analyze the factors influencing water preference studies.

---

Definitions:

Defective Condition

A condition that makes a product unreasonably dangerous to the consumer, user, or property. See product liability.

Unreasonably Dangerous

This term describes a product or condition that poses a significant risk of injury to individuals under normal use or foreseeable misuse, beyond what would be expected by the ordinary consumer.

Fair Credit Billing Act

A United States federal law designed to protect consumers from unfair billing practices and to provide a mechanism for addressing billing errors in "open-end" credit accounts, such as credit card or charge card accounts.

Billing Disputes

Conflicts between customers and service providers over charges, fees, or the accuracy of accounts receivable.