Use This Information,along with Its Associated Sensitivity Report,to Answer the Following

question 25

Multiple Choice

Use this information,along with its associated Sensitivity Report,to answer the following questions.
A production manager wants to determine how many units of each product to produce weekly to maximize weekly profits.Production requirements for the products are shown in the following table.
$$\begin{array} { | c | c | c | c | } \hline \underline { \text { Product } } & \frac { \text { Material 1 } } { ( \mathrm { lbs } ) } & \frac { \text { Material 2 } } { ( \mathrm { lbs } . ) } & \text { Labor (hours) } \\\hline \underline { \underline { \mathrm { A } } } & \underline { 3 } & \underline { 2 } & \underline { 4 } \\\hline \underline { \mathrm { B } } & \underline { 1 } & \underline { 4 } & \underline { 2 } \\\hline \underline { \mathrm { C } } & \underline { 5 } & \underline { \text { none } } & \underline { 3.5 } \\\hline\end{array}$$
Material 1 costs $7 a pound,material 2 costs $5 a pound,and labor costs $15 per hour.Product A sells for $101 a unit,product B sells for $67 a unit,and product C sells for $97.50 a unit.Each week there are 300 pounds of material 1;400 pounds of material 2;and 200 hours of labor.The output of product A should not be more than one-half of the total number of units produced.Moreover,there is a standing order of 10 units of product C each week.
$$\begin{array}{l}\text { Formulation }\\\begin{array} { l l } \ { \text { Max } } & 10 \mathrm {~A} + 10 \mathrm {~B} + 10 \mathrm { C } \\\text { Subject to: } & \\& 3 \mathrm {~A} + \mathrm { B } + 5 \mathrm { C } \leq 300 \text { (constraint \#1) } \\& 2 \mathrm {~A} + 4 \mathrm {~B} \leq 400 \text { (constraint \#2) } \\& 4 \mathrm {~A} + 2 \mathrm {~B} + 3.5 \mathrm { C } \leq 200 \text { (constraint \#3) } \\& \mathrm { C } \geq 10 \text { (constraint \#4) } \\& \mathrm { A } , \mathrm { B } , \mathrm { C } \geq 0\end{array}\end{array}$$

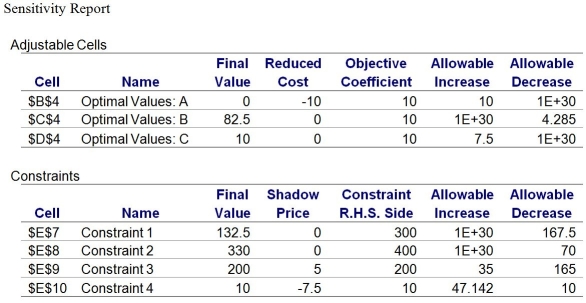
-Suppose that the objective function coefficient for product C increases by $8.What impact will this have on the current values of the optimal solution?

---

Definitions:

One-Line Consolidation

A method of including a subsidiary's information in a parent company's financial statements by a single line representing the investment's net value.

Consolidation

The process of combining the financial statements of a parent company with those of its subsidiaries to present the accounts as if the group of companies was a single entity.

Cost Method

An accounting technique used to record investments at their original purchase cost, adjusting for dividends received and not for changes in market value.

Equity Method

An accounting method for recording investments in which the investor recognizes income from the investee in proportion to its share of the investee’s profit or loss.