Use This Information,along with Its Associated Sensitivity Report,to Answer the Following

question 44

Multiple Choice

Use this information,along with its associated Sensitivity Report,to answer the following questions.
A production manager wants to determine how many units of each product to produce weekly to maximize weekly profits.Production requirements for the products are shown in the following table.
$$\begin{array} { | c | c | c | c | } \hline \underline { \text { Product } } & \frac { \text { Material 1 } } { ( \mathrm { lbs } ) } & \frac { \text { Material 2 } } { ( \mathrm { lbs } . ) } & \text { Labor (hours) } \\\hline \underline { \underline { \mathrm { A } } } & \underline { 3 } & \underline { 2 } & \underline { 4 } \\\hline \underline { \mathrm { B } } & \underline { 1 } & \underline { 4 } & \underline { 2 } \\\hline \underline { \mathrm { C } } & \underline { 5 } & \underline { \text { none } } & \underline { 3.5 } \\\hline\end{array}$$
Material 1 costs $7 a pound,material 2 costs $5 a pound,and labor costs $15 per hour.Product A sells for $101 a unit,product B sells for $67 a unit,and product C sells for $97.50 a unit.Each week there are 300 pounds of material 1;400 pounds of material 2;and 200 hours of labor.The output of product A should not be more than one-half of the total number of units produced.Moreover,there is a standing order of 10 units of product C each week.
$$\begin{array}{l}\text { Formulation }\\\begin{array} { l l } \ { \text { Max } } & 10 \mathrm {~A} + 10 \mathrm {~B} + 10 \mathrm { C } \\\text { Subject to: } & \\& 3 \mathrm {~A} + \mathrm { B } + 5 \mathrm { C } \leq 300 \text { (constraint \#1) } \\& 2 \mathrm {~A} + 4 \mathrm {~B} \leq 400 \text { (constraint \#2) } \\& 4 \mathrm {~A} + 2 \mathrm {~B} + 3.5 \mathrm { C } \leq 200 \text { (constraint \#3) } \\& \mathrm { C } \geq 10 \text { (constraint \#4) } \\& \mathrm { A } , \mathrm { B } , \mathrm { C } \geq 0\end{array}\end{array}$$

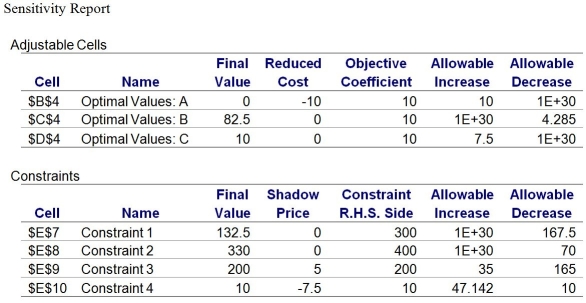
-Suppose that we force the production of one unit of product A.The new objective function value will be

---

Definitions:

Nondeclarative Memory

The subsystem within long-term memory that stores motor skills, habits, and simple classically conditioned responses; also called implicit memory.

Episodic Memory

A type of long-term memory that involves the recollection of specific events, situations, and experiences from an individual's life.

Depth Of Processing

A theory referring to how deeply information is processed and thought about, which influences how well it is remembered.

Craik And Lockhart's

Refers to the Levels of Processing theory of memory, proposing that memory retention depends on the depth of processing an item.