Professor Nightsoils Utility Function Is U N (B N, P

q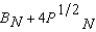uestion 25

Multiple Choice

Professor Nightsoils utility function is U N (B N, P N ) = and Dean Interfaces utility function is U I (B I, P I ) = 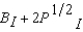, where B N and B I are the number of bromides and P N and P I are the number of platitudes consumed by Nightsoil and Interface respectively. If Nightsoils initial endowment is 4 bromides and 10 platitudes and if Interfaces initial endowment is 3 bromides and 15 platitudes, then at any Pareto efficient allocation in which both consume positive amounts of both goods,

• A) Interface consumes 3.50 bromides.
• B) Nightsoil consumes the same ratio of bromides to platitudes as Interface.
• C) Interface consumes 2 bromides.
• D) Interface consumes 5 platitudes.
• E) Interface consumes 3 bromides.

---

Definitions:

Population Mean

The total sum of all the values in a population divided by the number of values in that population, serving as a measure of central tendency.

Point Estimate

A single value given as an estimate of a population parameter derived from a sample.

Simple Random Samples

A subset of individuals chosen from a larger set such that every individual has an equal chance of being selected.

Random Samples

Samples chosen from a larger set or population where each individual or event has an equal chance of being selected.