(See Problem 2

question 1

Multiple Choice

(See Problem 2.) Willy's only source of wealth is his chocolate factory. He has the utility function 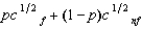, where p is the probability of a flood, 1 - p is the probability of no flood, and c_f and c_nf are his wealth contingent on a flood and on no flood, respectively. The probability of a flood is p = . The value of Willy's factory is $500,000 if there is no flood and 0 if there is a flood. Willy can buy insurance where if he buys $x worth of insurance, he must pay the insurance company $ 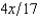whether there is a flood or not, but he gets back $x from the company if there is a flood. Willy should buy

• A) enough insurance so that if there is a flood, after he collects his insurance, his wealth will be the same whether there is a flood or not.
• B) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there is no flood.
• C) no insurance since the cost per dollar of insurance exceeds the probability of a flood.
• D) .enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there is no flood.
• E) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there is no flood

---

Definitions:

Supposing That

An expression used to introduce a hypothesis or an assumption for the sake of argument or analysis.

Unless

A conjunction used to indicate that a particular situation would occur only if there's an exception or condition not met.

Just In Case

A phrase used to describe a precautionary action taken to prepare for a possible future event or circumstance.

Conditional

A logical statement that has an if-then structure, implying that if one condition is met, then another condition follows.