A Grass Seed Company Conducts a Study to Determine the Relationship

question 24

Multiple Choice

A grass seed company conducts a study to determine the relationship between the density of seeds planted (in pounds per 500 sq ft) and the quality of the resulting lawn.Eight similar plots of land are selected and each is planted with a particular density of seed.One month later the quality of each lawn is rated on a scale of 0 to 100.The regression analysis and summary statistics are given below.A 99% prediction interval for the lawn quality of a lawn sown with a seed density of 2.9 was determined to be (10.6,82.0) .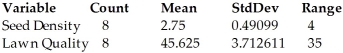
Dependent variable is: Lawn Quality
R-squared = 36.0%
S = 9.073602 with 8 - 2 = 6 degrees of freedom

• A)Based on this regression,we are 99% confident that the mean seed density will increase between 10.6 and 82.0 for each additional point of lawn quality over 2.9 pounds.
• B)Based on this regression,we are 99% confident that the mean lawn quality will increase between 10.6 and 82.0 for each additional pound of seed density over 2.9 pounds.
• C)Based on this regression,we are 99% confident that a lawn with a seed density of 2.9 pounds per 500 square feet will have a lawn quality between 10.6 and 82.0.
• D)Based on this regression,we are 99% confident that the mean lawn quality for lawns with a seed density of 2.9 pounds per 500 square feet will be between 10.6 and 82.0.
• E)Based on this regression,we know that 99% of all random samples will have a lawn quality between 10.6 and 82.0.

---

Definitions:

Crisis Management

The process by which an organization deals with a disruptive and unexpected event that threatens to harm its operations or stakeholders.

Crisis Situation

An emergency condition that poses a significant threat or requires immediate attention and action.

Structured Problems

Issues that are easily defined and have a clear, standardized solution procedure.

Systematic Decisions

Choices made based on a process that involves examining all available data, considering alternatives, and selecting the most suitable option in an organized manner.