Instruction 12 $\text { Regression statistics }$ $\text { ANOVA }$

question 11

True/False

Instruction 12.35
A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware. Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed:
$\text { Regression statistics }$
$\begin{array}{|l|l|}\hline \text { MultipleR } & 0.8691 \\\hline \text { R Square } & 0.7554 \\\hline \begin{array}{l}\text { Adjusted R } \\\text { Square }\end{array} & 0.7467 \\\hline \text { Standard Error } & 44.4765 \\\hline \text { Observations } & 30.0000\\\hline \end{array}$

$\text { ANOVA }$
$\begin{array}{|l|l|l|l|l|l|}\hline & d f & S S & M S & F & \begin{array}{l}\text { Significance } \\F\end{array} \\\hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\\hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\\hline \text { Total } & 29 & 226451.3503 & & & \\\hline\end{array}$

$\begin{array}{|l|l|l|l|l|l|l|}\hline & \text { Coefficients } & \begin{array}{l}\text { Standard } \\\text { Error }\end{array} & \text { t Stat } & p \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\\hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \\\hline\end{array}$



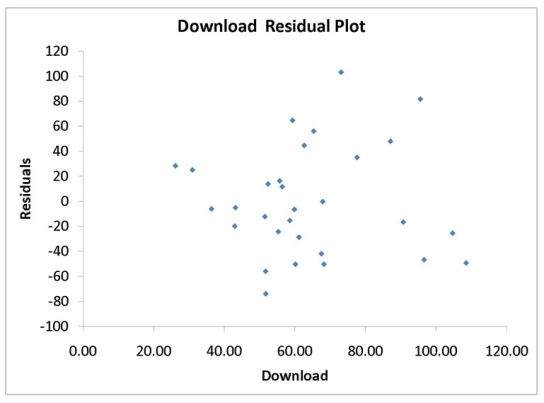
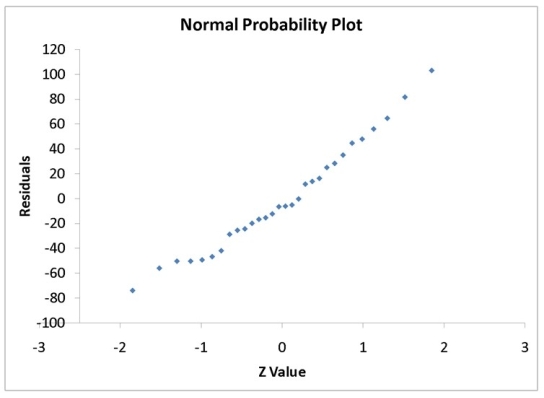
-Referring to Instruction 12.35,the null hypothesis for testing whether there is a linear relationship between revenue and number of downloads is 'There is no linear relationship between revenue and number of downloads'.

---

Definitions:

Additional Financing

Funds that are raised by a company through borrowing or issuing new equity, in addition to its existing capital.

Asset Turnover

A financial ratio that measures the efficiency of a company's use of its assets in generating sales revenue; the higher the turnover, the better.

Current Ratio

An indicator of a company's ability to meet short-term debt obligations; calculated by dividing current assets by current liabilities.

Fixed Assets

Fixed assets are long-term tangible assets that are used in the operations of a business and are not expected to be consumed or converted into cash within a year.