Instruction 12 $\text { Regression statistics }$ $\text { ANOVA }$

question 14

Multiple Choice

Instruction 12.17
A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware. Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed:
$\text { Regression statistics }$
$\begin{array}{|l|l|}\hline \text { MultipleR } & 0.8691 \\\hline \text { R Square } & 0.7554 \\\hline \begin{array}{l}\text { Adjusted R } \\\text { Square }\end{array} & 0.7467 \\\hline \text { Standard Error } & 44.4765 \\\hline \text { Observations } & 30.0000\\\hline \end{array}$

$\text { ANOVA }$
$\begin{array}{|l|l|l|l|l|l|}\hline & d f & S S & M S & F & \begin{array}{l}\text { Significance } \\F\end{array} \\\hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\\hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\\hline \text { Total } & 29 & 226451.3503 & & & \\\hline\end{array}$

$\begin{array}{|l|l|l|l|l|l|l|}\hline & \text { Coefficients } & \begin{array}{l}\text { Standard } \\\text { Error }\end{array} & \text { t Stat } & p \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\\hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \\\hline\end{array}$

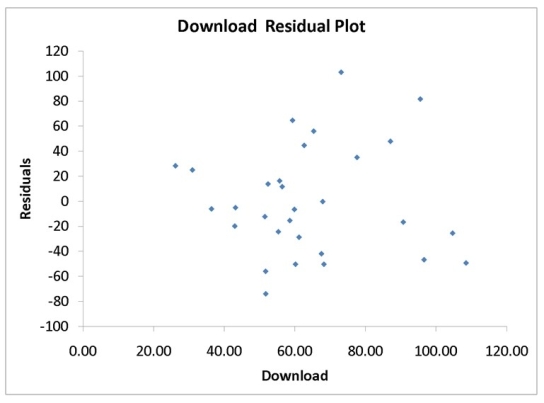
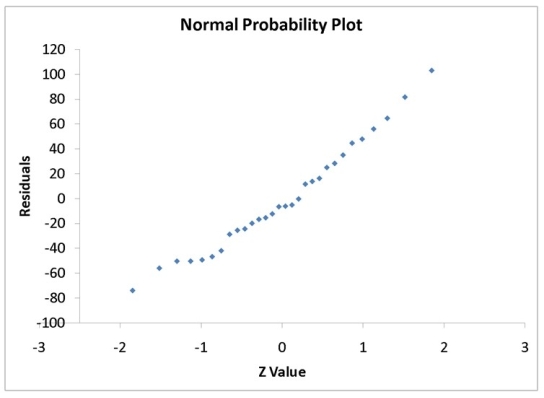
-Referring to Instruction 12.17,which of the following is the correct interpretation for the coefficient of determination?

• A) 74.67% of the variation in revenue can be explained by the variation in the number of downloads.
• B) 75.54% of the variation in revenue can be explained by the variation in the number of downloads.
• C) 75.54% of the variation in the number of downloads can be explained by the variation in revenue.
• D) 74.67% of the variation in the number of downloads can be explained by the variation in revenue.

---

Definitions:

Federal Procurement

Federal procurement involves the process by which government departments or agencies purchase goods, services, and works from the private sector.

Offshore Sourcing

The procurement of goods or services from suppliers located in countries other than the buyer's, often for cost saving purposes.

Global Supplier

A supplier that provides goods or services to companies in multiple countries, often involved in international trade.

Domestic Suppliers

Companies that provide goods or services within the same country as the company purchasing from them.