Instruction 12 $\text { Regression statistics }$ $\text { ANOVA }$

question 61

Short Answer

Instruction 12.35
A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware. Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed:
$\text { Regression statistics }$
$\begin{array}{|l|l|}\hline \text { MultipleR } & 0.8691 \\\hline \text { R Square } & 0.7554 \\\hline \begin{array}{l}\text { Adjusted R } \\\text { Square }\end{array} & 0.7467 \\\hline \text { Standard Error } & 44.4765 \\\hline \text { Observations } & 30.0000\\\hline \end{array}$

$\text { ANOVA }$
$\begin{array}{|l|l|l|l|l|l|}\hline & d f & S S & M S & F & \begin{array}{l}\text { Significance } \\F\end{array} \\\hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\\hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\\hline \text { Total } & 29 & 226451.3503 & & & \\\hline\end{array}$

$\begin{array}{|l|l|l|l|l|l|l|}\hline & \text { Coefficients } & \begin{array}{l}\text { Standard } \\\text { Error }\end{array} & \text { t Stat } & p \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\\hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \\\hline\end{array}$



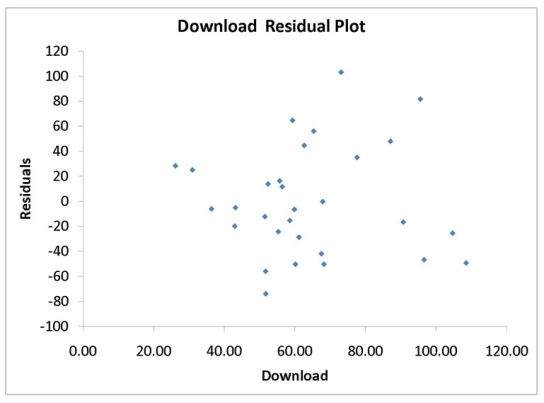
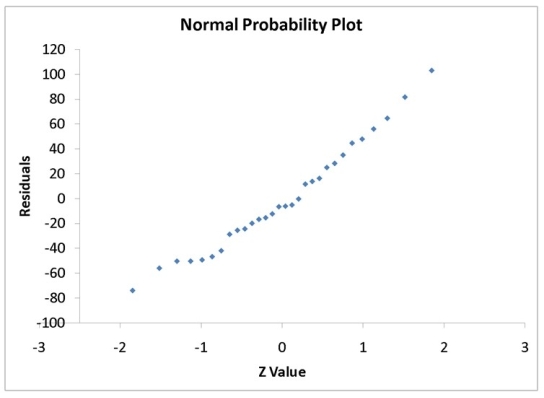
-Referring to Instruction 12.35,what is the critical value for testing whether there is a linear relationship between revenue and the number of downloads at a 5% level of significance?

Understand the significance of sustainable practices in marketing strategies.

Grasp the essentials of a visionary organization including its mission, vision, and value proposition.

Understand the role and impact of effective leadership in virtual and team-based organizations.

Recognize the importance of physical and virtual spaces in facilitating team communication.

---

Definitions:

Experience Curve

A concept that suggests that as a company gains experience in producing a product or service, its unit production costs decrease due to learning and efficiencies.

Cumulative Output

The total amount of product or work produced over a specific period.

Fixed Percent

A predetermined percentage rate applied in various financial and operational contexts, such as investment returns or budget allocations.

Varying Percent

Describes the difference in percentage rates, often used in finance and statistics, to compare changes over time or between different entities.