Consider the Following Parametric Linear Programming Problem,where the Parameter Must Be Nonnegative: Maximize Z
Consider the following parametric linear programming problem,where the parameter must be nonnegative: Maximize Z( )= (5 + 2 )x1 + (2 - )x2 + (3 + )x3,subject to 4x1 + x2 ≥ 5 + 5 , 3x1 + x2 + 2x3 = 10 - 10 ,x1 ≥ 0,x2 ≥ 0,x3 ≥ 0.Let x4 be the surplus variable for the first functional constraint,and let 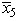 and
and  be the artificial variables for the respective functional constraints.After we apply the simplex method with the Big M method and with = 0,the final simplex tableau is
be the artificial variables for the respective functional constraints.After we apply the simplex method with the Big M method and with = 0,the final simplex tableau is 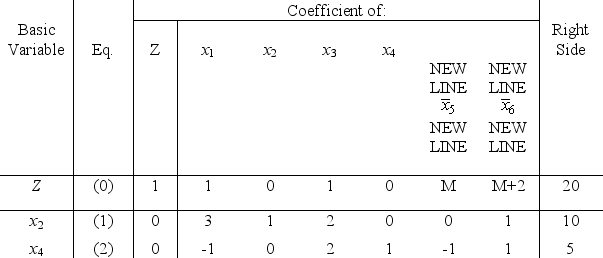
(a)Use the fundamental insight (Sec.5.3 in the textbook)to revise this tableau to reflect the inclusion of the parameter in the original model.Show the complete tableau needed to apply the feasibility test and the optimality test for any value of .Express the corresponding basic solution (and Z)as a function of .
(b)Determine the range of nonnegative values of over which this basic solution is feasible.
(c)Determine the range of nonnegative values of over which this basic solution is both feasible and optimal.Determine the best choice of over this range.
Definitions:
Income Tax Overpayment
A situation where an individual or entity has paid more income tax to the government than was actually owed.
Canada Revenue Agency
The federal agency responsible for administering tax laws and various social and economic benefit and incentive programs delivered through the tax system for the Government of Canada.
Simple Interest
A method of calculating interest where the charge is based on the original principal amount and does not compound.
Principal Amount
The original sum of money lent in a loan or invested, excluding any interest or profits.
Q2: According to the equation of exchange,the total
Q4: A depreciation of the dollar results in
Q5: At the end of the conceptual design
Q35: An expenditure-reducing policy would consist of a
Q37: The relationship between the Rent Item and
Q47: What is end-user computing? Why has end-user
Q51: A problem that economic policy makers confront
Q67: What is the emphasis of the first
Q72: Which business process reengineering principle is applied
Q78: IMF drawings,swap arrangements,buffer stock facility,and compensatory financing