Consider the Following Parametric Linear Programming Problem,where the Parameter Must Be Nonnegative: Maximize Z
Consider the following parametric linear programming problem,where the parameter must be nonnegative: Maximize Z( )= (5 + 2 )x1 + (2 - )x2 + (3 + )x3,subject to 4x1 + x2 ≥ 5 + 5 , 3x1 + x2 + 2x3 = 10 - 10 ,x1 ≥ 0,x2 ≥ 0,x3 ≥ 0.Let x4 be the surplus variable for the first functional constraint,and let 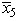 and
and  be the artificial variables for the respective functional constraints.After we apply the simplex method with the Big M method and with = 0,the final simplex tableau is
be the artificial variables for the respective functional constraints.After we apply the simplex method with the Big M method and with = 0,the final simplex tableau is 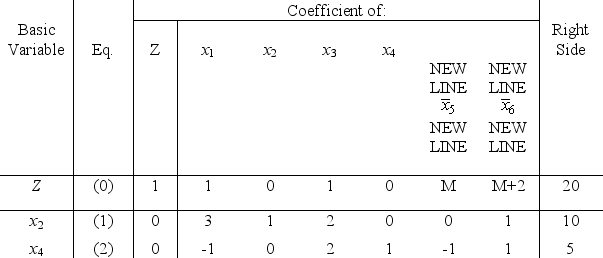
(a)Use the fundamental insight (Sec.5.3 in the textbook)to revise this tableau to reflect the inclusion of the parameter in the original model.Show the complete tableau needed to apply the feasibility test and the optimality test for any value of .Express the corresponding basic solution (and Z)as a function of .
(b)Determine the range of nonnegative values of over which this basic solution is feasible.
(c)Determine the range of nonnegative values of over which this basic solution is both feasible and optimal.Determine the best choice of over this range.
Definitions:
Sexual Intercourse
A physical act between individuals that involves genital contact and the exchange of sexual fluids, often leading to sexual gratification.
Gender Neutral
A term that does not specify a gender, used to avoid assumptions or discrimination based on binary gender categories.
Androgynous
Exhibiting both traditional male and female characteristics, making it difficult to classify someone strictly as male or female based on appearances alone.
Postgendered
Referring to a society or a concept where traditional gender roles and identity markers are transcended, allowing individuals to define themselves beyond male or female categories.
Q21: An REA diagram for the production cycle
Q24: Refer to Exhibit 16.1.To help drive the
Q28: In 1973 the major industrial countries terminated
Q47: The par values of most developing-country currencies
Q57: The _ relationship between Skills and Recruiting
Q60: The relationship between the Disburse Cash and
Q64: All of the four categories of output
Q68: Refer to Table 15.1.If monetary authorities fix
Q72: During the gold standard era,the "rules of
Q75: A surplus nation can reduce its payments