Solved

Instruction 12-12
the Manager of the Purchasing Department of a Large

question 34

Multiple Choice

Instruction 12-12
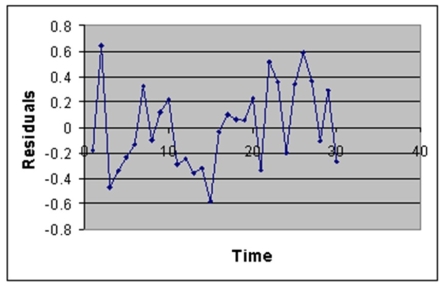
The manager of the purchasing department of a large savings and loan organization would like to develop a model to predict the amount of time (measured in hours) it takes to record a loan application.Data are collected from a sample of 30 days,and the number of applications recorded and completion time in hours is recorded.Below is the regression output:
$\begin{array}{l}\begin{array} { l r } \hline { \text { Regression Statistics } } \\\hline \text { Multiple R } & 0.9447 \\\text { R Square } & 0.8924 \\\text { Adjusted R } & 0.8886 \\\text { Square } & \\\text { Standard } & 0.3342 \\\text { Error } & 30 \\\text { Observations } & \\\hline\end{array}\\\text { ANOVA }\\\begin{array} { l r r r r r } \hline & d f & { \text { SS } } & { \text { MS } } & F & { \begin{array} { c } \text { Significance } \\F\end{array} } \\\hline \text { Regression } & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm { E } - 15 \\\text { Residual } & 28 & 3.1282 & 0.1117 & & \\\text { Total } & 29 & 29.072 & & & \\\hline\end{array}\\\begin{array} { l r r r r r r } \hline & \text { Coefficients } & \begin{array} { c } \text { Standard } \\\text { Error }\end{array} & t \text { Stat } & P \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \begin{array} { l } \text { Intercept } \\\text { Applications } \\\text { Recorded }\end{array} & 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\\hline\end{array}\end{array}$ Note: 4.3946E-15 is 4.3946 x 10^-15.
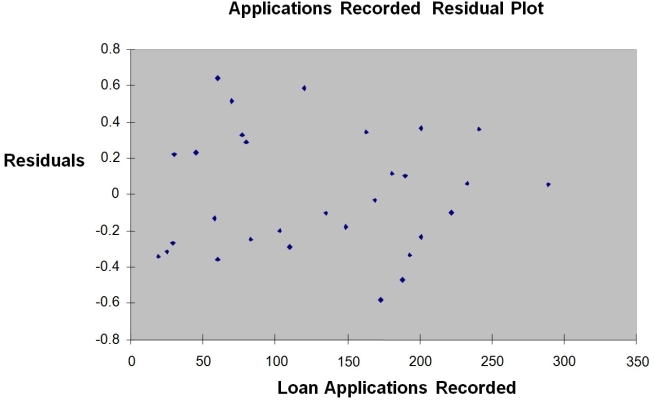
$Instruction 12-12 The manager of the purchasing department of a large savings and loan organization would like to develop a model to predict the amount of time (measured in hours) it takes to record a loan application.Data are collected from a sample of 30 days,and the number of applications recorded and completion time in hours is recorded.Below is the regression output: \begin{array}{l} \begin{array} { l r } \hline { \text { Regression Statistics } } \\ \hline \text { Multiple R } & 0.9447 \\ \text { R Square } & 0.8924 \\ \text { Adjusted R } & 0.8886 \\ \text { Square } & \\ \text { Standard } & 0.3342 \\ \text { Error } & 30 \\ \text { Observations } & \\ \hline \end{array}\\ \text { ANOVA }\\ \begin{array} { l r r r r r } \hline & d f & { \text { SS } } & { \text { MS } } & F & { \begin{array} { c } \text { Significance } \\ F \end{array} } \\ \hline \text { Regression } & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm { E } - 15 \\ \text { Residual } & 28 & 3.1282 & 0.1117 & & \\ \text { Total } & 29 & 29.072 & & & \\ \hline \end{array}\\ \begin{array} { l r r r r r r } \hline & \text { Coefficients } & \begin{array} { c } \text { Standard } \\ \text { Error } \end{array} & t \text { Stat } & P \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \begin{array} { l } \text { Intercept } \\ \text { Applications } \\ \text { Recorded } \end{array} & 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \hline \end{array} \end{array} Note: 4.3946E-15 is 4.3946 x 10<sup>-15</sup>. -Referring to Instruction 12-12,the error sum of squares (SSE) of the above regression is A) 0.1117. B) 29.0720. C) 25.9438. D) 3.1282.$ $Instruction 12-12 The manager of the purchasing department of a large savings and loan organization would like to develop a model to predict the amount of time (measured in hours) it takes to record a loan application.Data are collected from a sample of 30 days,and the number of applications recorded and completion time in hours is recorded.Below is the regression output: \begin{array}{l} \begin{array} { l r } \hline { \text { Regression Statistics } } \\ \hline \text { Multiple R } & 0.9447 \\ \text { R Square } & 0.8924 \\ \text { Adjusted R } & 0.8886 \\ \text { Square } & \\ \text { Standard } & 0.3342 \\ \text { Error } & 30 \\ \text { Observations } & \\ \hline \end{array}\\ \text { ANOVA }\\ \begin{array} { l r r r r r } \hline & d f & { \text { SS } } & { \text { MS } } & F & { \begin{array} { c } \text { Significance } \\ F \end{array} } \\ \hline \text { Regression } & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm { E } - 15 \\ \text { Residual } & 28 & 3.1282 & 0.1117 & & \\ \text { Total } & 29 & 29.072 & & & \\ \hline \end{array}\\ \begin{array} { l r r r r r r } \hline & \text { Coefficients } & \begin{array} { c } \text { Standard } \\ \text { Error } \end{array} & t \text { Stat } & P \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \begin{array} { l } \text { Intercept } \\ \text { Applications } \\ \text { Recorded } \end{array} & 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \hline \end{array} \end{array} Note: 4.3946E-15 is 4.3946 x 10<sup>-15</sup>. -Referring to Instruction 12-12,the error sum of squares (SSE) of the above regression is A) 0.1117. B) 29.0720. C) 25.9438. D) 3.1282.$
-Referring to Instruction 12-12,the error sum of squares (SSE) of the above regression is

Definitions:

Processed Further

Refers to additional operations or treatments applied to a product after its initial processing stage.

Financial Advantage

The benefit gained in a financial aspect, which can refer to lower costs, greater returns, or other financial gains.

Industrial Fiber

Synthetic or natural fibers used for commercial and industrial applications, such as manufacturing textiles, composites, and structural materials.

Molasses

is a thick, dark syrup produced as a byproduct of refining sugar cane or sugar beets into sugar, often used in baking and cooking.

Instruction 12-12 the Manager of the Purchasing Department of a Large

Definitions:

Instruction 12-12
the Manager of the Purchasing Department of a Large