A Mass on a Smooth Tabletop Is Attached to a Spring

question 25

Multiple Choice

A mass on a smooth tabletop is attached to a spring, as shown in the figure. The coordinate system has been chosen so that the equilibrium position of the mass corresponds to $$s = 0$$ . Assume that the simple harmonic motion is described by the equation $$s = 5 \cos \left( \frac { \pi t } { 3 } \right)$$ , where s is in centimeters and t is in seconds. Determine which table describes the s-coordinate of the mass at each of the following times: $$t =$$ 0 sec, 0.5 sec, 1 sec, and 2 sec. (One of these coordinates will involve a radical sign; for this case, use a calculator and round the final answer to two decimal places.)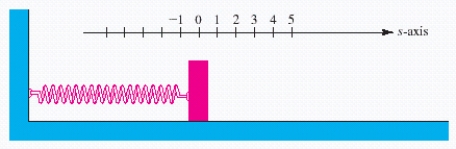

• A) \[\begin{array} { | c | c | } \hline \text { time (sec) } & \text { s-coordinate(cm) } \\ \hline 0 & 5 \\ \hline 0.5 & 4.33 \\ \hline 1 & 2.5 \\ \hline 2 & 2.5 \\ \hline \end{array}\]
• B) \[\begin{array} { | c | c | } \hline \text { time (sec) } & \text { s-coordinate(cm) } \\ \hline 0 & - 2.5 \\ \hline 0.5 & 4.33 \\ \hline 1 & 2.5 \\ \hline 2 & 5 \\ \hline \end{array}\]
• C) \[\begin{array} { | c | c | } \hline \text { time (sec) } & \text { s-coordinate(cm) } \\ \hline 0 & 5 \\ \hline 0.5 & 4.33 \\ \hline 1 & 2.5 \\ \hline 2 & - 2.5 \\ \hline \end{array}\]
• D) \[\begin{array} { | c | c | } \hline \text { time (sec) } & \text { s-coordinate(cm) } \\ \hline 0 & 2.5 \\ \hline 0.5 & 4.33 \\ \hline 1 & 5 \\ \hline 2 & - 2.5 \\ \hline \end{array}\]
• E) \[\begin{array} { | c | c | } \hline \text { time (sec) } & \text { s-coordinate(cm) } \\ \hline 0 & 5 \\ \hline 0.5 & 2.5 \\ \hline 1 & 4.33 \\ \hline 2 & - 2.5 \\ \hline \end{array}\]

Identify and describe the features of SharePoint Online that facilitate document management and collaboration.

Distinguish between different SharePoint Online features and their appropriate uses in a collaborative project environment.

Understand and apply the principles of accounting for asset acquisition and disposal, including cost determination and journal entry preparation.

Calculate and record depreciation expense using different methods (straight-line, double-declining-balance, units-of-production).

---

Definitions:

Practicing Hard

The act of engaging in intensive and focused training or rehearsal to improve performance in a specific skill or task.

Children's Friendships

Relationships formed between children that are characterized by mutual affection, trust, and support, playing a crucial role in their social and emotional development.

Nonhostile Social Comparison

The act of comparing oneself with others in a way that is not competitive or antagonistic, often for self-improvement or learning purposes.

Hypercompetitiveness

An excessive emphasis on competition and winning in all aspects of life, often at the expense of personal relationships and ethical standards.