The Graph of an Equation of a Sine Wave Is $\text { amplitude } = 3 , \quad \text { period } = \pi , \quad \text { phaseshift } = - \frac { \pi } { 4 }$

question 4

Multiple Choice

The graph of an equation of a sine wave is shown in the figure. Find the amplitude, period, and phase shift.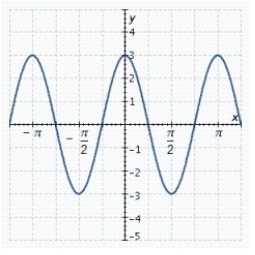

• A) \(\text { amplitude } = 3 , \quad \text { period } = \pi , \quad \text { phaseshift } = - \frac { \pi } { 4 }\) , \(y = 3 \sin \left( 2 x + \frac { \pi } { 2 } \right)\)
• B) \(\text { amplitude } = 6 , \quad \text { period } = \pi , \quad \text { phaseshift } = \frac { \pi } { 8 }\) , \(y = 6 \sin \left( 2 x + \frac { \pi } { 2 } \right)\)
• C) \(\text { amplitude } = 4 , \quad \text { period } = \pi , \quad \text { phaseshift } = - \frac { \pi } { 6 }\) , \(y = 4 \sin \left( 2 x + \frac { \pi } { 2 } \right)\)
• D) \(\text { amplitude } = 3 , \quad \text { period } = \pi , \quad \text { phaseshift } = - \frac { \pi } { 4 }\) , \(y = 3 \cos \left( 2 x + \frac { \pi } { 2 } \right)\)
• E) \(\text { amplitude } = 6 , \quad \text { period } = \pi , \quad \text { phaseshift } = \frac { \pi } { 4 }\) , \(y = 6 \cos \left( 2 x + \frac { \pi } { 2 } \right)\)

Identify the impact of sudden changes in stimulus intensity on attention and reaction.

Recognize how environmental changes affect color perception.

Explain various persuasion techniques, including the door-in-the-face technique.

Trace the path of a visual stimulus from source to perception, illustrating the complex integration of sensory information.