Solved

Let , Be Functions and Let

question 32

Multiple Choice

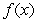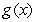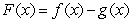Let Let , be functions and let . Consider the following statement: If and exist then also exists. To prove this statement we should use: A) The statement is not true. B) The Product Rule applied to and . C) The Quotient Rule applied to and . D) The Sum Rule applied to and . E) None of the above. , be functions and let Let , be functions and let . Consider the following statement: If and exist then also exists. To prove this statement we should use: A) The statement is not true. B) The Product Rule applied to and . C) The Quotient Rule applied to and . D) The Sum Rule applied to and . E) None of the above. . Consider the following statement:
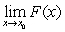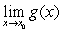If Let , be functions and let . Consider the following statement: If and exist then also exists. To prove this statement we should use: A) The statement is not true. B) The Product Rule applied to and . C) The Quotient Rule applied to and . D) The Sum Rule applied to and . E) None of the above. and exist then also Let , be functions and let . Consider the following statement: If and exist then also exists. To prove this statement we should use: A) The statement is not true. B) The Product Rule applied to and . C) The Quotient Rule applied to and . D) The Sum Rule applied to and . E) None of the above. 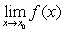exists.
To prove this statement we should use:

Definitions:

Counterconditioning

A behavior therapy procedure that uses classical conditioning to evoke new responses to stimuli that are triggering unwanted behaviors; includes exposure therapies and aversive conditioning.

Unwanted Responses

Reactions or behaviors that are not desired or intended, often occurring in a psychological or physiological context.

New Responses

Fresh or novel reactions or actions made in response to stimuli or situations that have not been encountered before.

Insight Therapies

A variety of therapies that aim to improve psychological functioning by increasing the client’s awareness of underlying motives and defenses.