A Second Order Differential Equation Can Be Arranged to the Form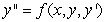

question 19

Multiple Choice

A second order differential equation can be arranged to the form , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor-series expansion of a function y(x) is 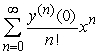, one can differentiate the rearranged second order differential equation to evaluate coefficients in the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What is the coefficient of x⁴ in the Taylor polynomial expansion of the solution to the equation if the initial conditions are ?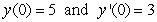

---

Definitions:

Painting Technique

The methodology or specific approach an artist uses when applying pigment to a surface, involving a variety of tools, mediums, and styles to achieve desired effects.

Chromatic Abstractionism

An artistic movement that focuses on the use of intense colors in abstract works, often to evoke emotions or express non-objective realities.

Color Fields

A style of abstract painting characterized by large, solid colors spread across or within a canvas, emphasizing the overall impact of color.

Zips

Elements frequently used in the paintings of Barnett Newman, consisting of vertical lines or "zips" that divide the canvas into sections and introduce a dynamic interplay of space.