The Mean of the Population ( 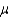)Is 200 on a Test

question 46

Multiple Choice

The mean of the population ( ) is 200 on a test that measures math skills of middle school students.The variance 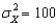.The test scores for the students in Mr.Petris's class at Suburban Middle School are given below.Use a rejection region with a probability of 5% only in the upper tail.What should you conclude?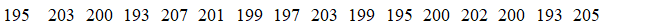

• A)Since the z-value falls within the region of rejection,we should conclude this sample mean likely represents some other population.
• B)Since the z-value does not fall within the region of rejection,we should not conclude this sample mean represents some other population.
• C)Since the z-value falls within the region of rejection,we should not conclude this sample mean represents some other population.
• D)Since the z-value does not fall within the region of rejection,we should conclude this sample mean likely represents some other population.

---

Definitions:

Public Interest

Public Interest refers to the welfare or well-being of the general public and society at large.

Assignable

A quality of a contract or right that allows it to be transferred from one party to another.

Third Party Rights

Rights that are granted to individuals or entities who are not a direct party to a contract or legal agreement but are affected by its provisions.

Delegation

The act of transferring to another person the authority to perform a particular task or function.