Examlex

Solved

The Following Table Shows the Annual Revenues (In Millions of Dollars)of

question 122

Essay

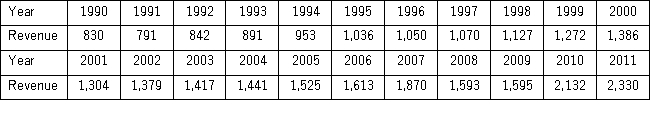The following table shows the annual revenues (in millions of dollars)of a pharmaceutical company over the period 1990-2011. The following table shows the annual revenues (in millions of dollars)of a pharmaceutical company over the period 1990-2011. The autoregressive models of order 1 and 2,y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + ε<sub>t</sub>,and y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + β<sub>2</sub>y<sub>t - 2</sub> + ε<sub>t</sub>,were applied on the time series to make revenue forecasts.The relevant parts of Excel regression outputs are given below. Model AR(1): Model AR(2): When for AR(1),H<sub>0</sub>: β<sub>0</sub> = 0 is tested against H<sub>A</sub>: β<sub>0</sub> ≠ 0,the p-value of this t test shown by Excel output is 0.9590.This could suggest that the model y<sub>t</sub> = β<sub>1</sub>y<sub>t</sub><sub>-1 </sub>+ ε<sub>t</sub> might be an alternative to the AR(1)model y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>.Excel partial output for this simplified model is as follows: Find the revenue forecast for 2012 through the use of y<sub>t</sub> = β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>. The autoregressive models of order 1 and 2,yt = β0 + β1yt - 1 + εt,and yt = β0 + β1yt - 1 + β2yt - 2 + εt,were applied on the time series to make revenue forecasts.The relevant parts of Excel regression outputs are given below.
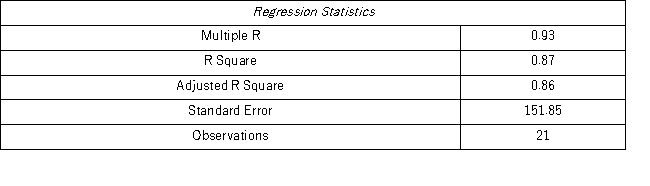
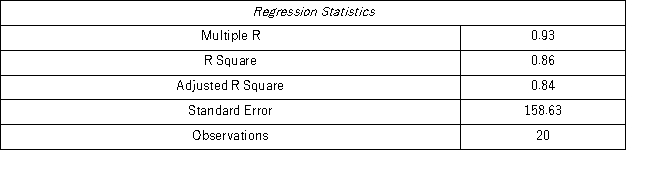
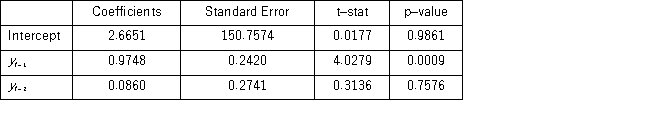Model AR(1): The following table shows the annual revenues (in millions of dollars)of a pharmaceutical company over the period 1990-2011. The autoregressive models of order 1 and 2,y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + ε<sub>t</sub>,and y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + β<sub>2</sub>y<sub>t - 2</sub> + ε<sub>t</sub>,were applied on the time series to make revenue forecasts.The relevant parts of Excel regression outputs are given below. Model AR(1): Model AR(2): When for AR(1),H<sub>0</sub>: β<sub>0</sub> = 0 is tested against H<sub>A</sub>: β<sub>0</sub> ≠ 0,the p-value of this t test shown by Excel output is 0.9590.This could suggest that the model y<sub>t</sub> = β<sub>1</sub>y<sub>t</sub><sub>-1 </sub>+ ε<sub>t</sub> might be an alternative to the AR(1)model y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>.Excel partial output for this simplified model is as follows: Find the revenue forecast for 2012 through the use of y<sub>t</sub> = β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>. The following table shows the annual revenues (in millions of dollars)of a pharmaceutical company over the period 1990-2011. The autoregressive models of order 1 and 2,y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + ε<sub>t</sub>,and y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + β<sub>2</sub>y<sub>t - 2</sub> + ε<sub>t</sub>,were applied on the time series to make revenue forecasts.The relevant parts of Excel regression outputs are given below. Model AR(1): Model AR(2): When for AR(1),H<sub>0</sub>: β<sub>0</sub> = 0 is tested against H<sub>A</sub>: β<sub>0</sub> ≠ 0,the p-value of this t test shown by Excel output is 0.9590.This could suggest that the model y<sub>t</sub> = β<sub>1</sub>y<sub>t</sub><sub>-1 </sub>+ ε<sub>t</sub> might be an alternative to the AR(1)model y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>.Excel partial output for this simplified model is as follows: Find the revenue forecast for 2012 through the use of y<sub>t</sub> = β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>. Model AR(2): The following table shows the annual revenues (in millions of dollars)of a pharmaceutical company over the period 1990-2011. The autoregressive models of order 1 and 2,y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + ε<sub>t</sub>,and y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + β<sub>2</sub>y<sub>t - 2</sub> + ε<sub>t</sub>,were applied on the time series to make revenue forecasts.The relevant parts of Excel regression outputs are given below. Model AR(1): Model AR(2): When for AR(1),H<sub>0</sub>: β<sub>0</sub> = 0 is tested against H<sub>A</sub>: β<sub>0</sub> ≠ 0,the p-value of this t test shown by Excel output is 0.9590.This could suggest that the model y<sub>t</sub> = β<sub>1</sub>y<sub>t</sub><sub>-1 </sub>+ ε<sub>t</sub> might be an alternative to the AR(1)model y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>.Excel partial output for this simplified model is as follows: Find the revenue forecast for 2012 through the use of y<sub>t</sub> = β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>. The following table shows the annual revenues (in millions of dollars)of a pharmaceutical company over the period 1990-2011. The autoregressive models of order 1 and 2,y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + ε<sub>t</sub>,and y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + β<sub>2</sub>y<sub>t - 2</sub> + ε<sub>t</sub>,were applied on the time series to make revenue forecasts.The relevant parts of Excel regression outputs are given below. Model AR(1): Model AR(2): When for AR(1),H<sub>0</sub>: β<sub>0</sub> = 0 is tested against H<sub>A</sub>: β<sub>0</sub> ≠ 0,the p-value of this t test shown by Excel output is 0.9590.This could suggest that the model y<sub>t</sub> = β<sub>1</sub>y<sub>t</sub><sub>-1 </sub>+ ε<sub>t</sub> might be an alternative to the AR(1)model y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>.Excel partial output for this simplified model is as follows: Find the revenue forecast for 2012 through the use of y<sub>t</sub> = β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>. When for AR(1),H0: β0 = 0 is tested against HA: β0 ≠ 0,the p-value of this t test shown by Excel output is 0.9590.This could suggest that the model yt = β1yt-1 + εt might be an alternative to the AR(1)model yt = β0 + β1yt-1 + εt.Excel partial output for this simplified model is as follows: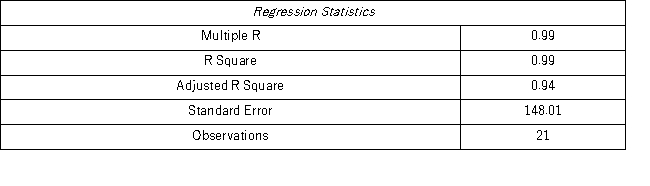 The following table shows the annual revenues (in millions of dollars)of a pharmaceutical company over the period 1990-2011. The autoregressive models of order 1 and 2,y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + ε<sub>t</sub>,and y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + β<sub>2</sub>y<sub>t - 2</sub> + ε<sub>t</sub>,were applied on the time series to make revenue forecasts.The relevant parts of Excel regression outputs are given below. Model AR(1): Model AR(2): When for AR(1),H<sub>0</sub>: β<sub>0</sub> = 0 is tested against H<sub>A</sub>: β<sub>0</sub> ≠ 0,the p-value of this t test shown by Excel output is 0.9590.This could suggest that the model y<sub>t</sub> = β<sub>1</sub>y<sub>t</sub><sub>-1 </sub>+ ε<sub>t</sub> might be an alternative to the AR(1)model y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>.Excel partial output for this simplified model is as follows: Find the revenue forecast for 2012 through the use of y<sub>t</sub> = β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>. The following table shows the annual revenues (in millions of dollars)of a pharmaceutical company over the period 1990-2011. The autoregressive models of order 1 and 2,y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + ε<sub>t</sub>,and y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + β<sub>2</sub>y<sub>t - 2</sub> + ε<sub>t</sub>,were applied on the time series to make revenue forecasts.The relevant parts of Excel regression outputs are given below. Model AR(1): Model AR(2): When for AR(1),H<sub>0</sub>: β<sub>0</sub> = 0 is tested against H<sub>A</sub>: β<sub>0</sub> ≠ 0,the p-value of this t test shown by Excel output is 0.9590.This could suggest that the model y<sub>t</sub> = β<sub>1</sub>y<sub>t</sub><sub>-1 </sub>+ ε<sub>t</sub> might be an alternative to the AR(1)model y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>.Excel partial output for this simplified model is as follows: Find the revenue forecast for 2012 through the use of y<sub>t</sub> = β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>. Find the revenue forecast for 2012 through the use of yt = β1yt-1 + εt.

Definitions:

Fixed Costs

Costs that remain constant regardless of the amount of goods produced or sold, including rent, wages, and insurance premiums.

Short Run

A time period in economics during which at least one input is fixed and cannot be changed by the business.

Monopolistically Competitive

Refers to a market structure where many firms sell products that are similar but not identical, allowing for some degree of market power in setting prices.

Average Total Cost

Average total cost is the total cost of production divided by the number of units produced, encompassing both fixed and variable costs.

Related Questions

Q22: Which of the following regression models is

Q29: The broad field of _ would most

Q30: A trading magazine wants to determine the

Q41: Which of the following statements is true

Q58: Joanna Robertson bought a share of XYZ

Q61: If the variance of the error term

Q78: A logistic model can be estimated with

Q110: It is believed that the sales volume

Q116: A simple linear regression of the return

Q135: In the sample regression equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4266/.jpg"