In the Case of Perfect Multicollinearity,OLS Is Unable to Calculate

question 58

Essay

In the case of perfect multicollinearity,OLS is unable to calculate the coefficients for the explanatory variables,because it is impossible to change one variable while holding all other variables constant.To see why this is the case,consider the coefficient for the first explanatory variable in the case of a multiple regression model with two explanatory variables: (small letters refer to deviations from means as in ).
Divide each of the four terms by 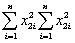to derive an expression in terms of regression coefficients from the simple (one explanatory variable)regression model.In case of perfect multicollinearity,what would be R2 from the regression of 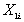on ? As a result,what would be the value of the denominator in the above expression for ?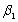

---

Definitions:

Fat Clients

Computing devices in client-server architecture that perform bulk of data processing operations themselves, rather than rely on a server.

Network Fails

Refers to instances when a network encounters errors or problems that prevent it from functioning correctly.

Binary Form

Binary Form is a way of structuring a piece of music in two related sections, both of which are usually repeated. This term is also used in computing to describe data represented in two states such as 0 and 1.

ALU

Arithmetic Logic Unit; a component of a computer processor that performs arithmetic and logical operations.