(Continuation from Chapter 4,number 6)The Neoclassical Growth Model Predicts That

question 18

Essay

(Continuation from Chapter 4,number 6)The neoclassical growth model predicts that for identical savings rates and population growth rates,countries should converge to the per capita income level.This is referred to as the convergence hypothesis.One way to test for the presence of convergence is to compare the growth rates over time to the initial starting level.
(a)The results of the regression for 104 countries were as follows: 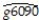= 0.019 - 0.0006 × RelProd60,R2= 0.00007,SER = 0.016
(0.004)(0.0073) where g6090 is the average annual growth rate of GDP per worker for the 1960-1990 sample period,and RelProd60 is GDP per worker relative to the United States in 1960.Numbers in parenthesis are heteroskedasticity robust standard errors.
Using the OLS estimator with homoskedasticity-only standard errors,the results changed as follows: 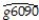= 0.019 - 0.0006×RelProd60,R2= 0.00007,SER = 0.016
(0.002)(0.0068)
Why didn't the estimated coefficients change? Given that the standard error of the slope is now smaller,can you reject the null hypothesis of no beta convergence? Are the results in the second equation more reliable than the results in the first equation? Explain.
(b)You decide to restrict yourself to the 24 OECD countries in the sample.This changes your regression output as follows (numbers in parenthesis are heteroskedasticity robust standard errors): 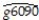= 0.048 - 0.0404 RelProd60,R2 = 0.82,SER = 0.0046
(0.004)(0.0063)
Test for evidence of convergence now.If your conclusion is different than in (a),speculate why this is the case.
(c)The authors of your textbook have informed you that unless you have more than 100 observations,it may not be plausible to assume that the distribution of your OLS estimators is normal.What are the implications here for testing the significance of your theory?

---

Definitions:

Low Probability Sample

A sampling method where individuals or elements have a low chance of being selected for participation in a study.

Representative Sample

A subset of a population carefully selected to reflect the characteristics of the larger group accurately, essential for valid and generalizable research findings.

Voluntary Response Sample

A sample which consists of individuals who choose themselves to participate in a survey, often leading to bias and unrepresentative samples.

Contingency Table

A Contingency Table is a statistical tool used to analyze the relationship between two or more variables, presenting the frequency distribution in a matrix format.