Let p be the success probability of a Bernoulli random variable Y,i.e. ,p = Pr(Y = 1).It can be shown that 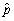 ,the fraction of successes in a sample,is asymptotically distributed N(p,
,the fraction of successes in a sample,is asymptotically distributed N(p, 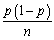 .Using the estimator of the variance of
.Using the estimator of the variance of 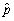 ,
, 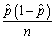 ,construct a 95% confidence interval for p.Show that the margin for sampling error simplifies to 1/
,construct a 95% confidence interval for p.Show that the margin for sampling error simplifies to 1/ 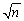 if you used 2 instead of 1.96 assuming,conservatively,that the standard error is at its maximum.Construct a table indicating the sample size needed to generate a margin of sampling error of 1%,2%,5% and 10%.What do you notice about the increase in sample size needed to halve the margin of error? (The margin of sampling error is 1.96×SE(
if you used 2 instead of 1.96 assuming,conservatively,that the standard error is at its maximum.Construct a table indicating the sample size needed to generate a margin of sampling error of 1%,2%,5% and 10%.What do you notice about the increase in sample size needed to halve the margin of error? (The margin of sampling error is 1.96×SE( 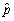 ))
))
Definitions:
Market Value
The present cost at which a service or asset is available for purchase or sale in a market setting.
Replacement Cost
The current cost to replace an asset with a similar one of equivalent utility and quality, without considering depreciation.
Selling Price
The amount of money for which a product or service is sold to customers.
Insurance Expense
Insurance expense refers to the cost incurred by an entity to obtain coverage against various risks, recorded as an expense in the financial statements.
Q4: Math SAT scores (Y)are normally distributed with
Q21: Consider the model Yi = β1Xi +
Q23: In the model Yi = β0 +
Q24: Your textbook gave an example of attempting
Q30: Let Y = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2833/.jpg" alt="Let Y
Q34: Among all unbiased estimators that are weighted
Q48: Imagine that you were told that the
Q48: The main advantage of using panel data
Q57: Misspecification of functional form of the regression
Q58: (Requires calculus. )Let Y be a Bernoulli