You Have Learned in One of Your Economics Courses That

question 64

Essay

You have learned in one of your economics courses that one of the determinants of per capita income (the "Wealth of Nations")is the population growth rate.Furthermore you also found out that the Penn World Tables contain income and population data for 104 countries of the world.To test this theory,you regress the GDP per worker (relative to the United States)in 1990 (RelPersInc)on the difference between the average population growth rate of that country (n)to the U.S.average population growth rate (nus )for the years 1980 to 1990.This results in the following regression output: 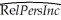= 0.518 - 18.831 × 18.831 × (n - nus),R2 = 0.522,SER = 0.197
(a)Interpret the results carefully.Is this relationship economically important?
(b)What would happen to the slope,intercept,and regression R2 if you ran another regression where the above explanatory variable was replaced by n only,i.e. ,the average population growth rate of the country? (The population growth rate of the United States from 1980 to 1990 was 0.009. )Should this have any effect on the t-statistic of the slope?
(c)31 of the 104 countries have a dependent variable of less than 0.10.Does it therefore make sense to interpret the intercept?

---

Definitions:

Catalyze

To accelerate a chemical reaction without being consumed or altered in the process.

Enzymes

Biologically derived entities that drastically increase the pace of essentially all chemical transformations within cell boundaries.

Exergonic Reaction

A chemical reaction that releases energy by light or heat, making it energetically favorable.

Free Energy

The portion of a system's energy that is able to perform work when temperature and pressure are uniform throughout the system.