(Advanced)Unbiasedness and Small Variance Are Desirable Properties of Estimators

question 33

Essay

(Advanced)Unbiasedness and small variance are desirable properties of estimators.However,you can imagine situations where a trade-off exists between the two: one estimator may be have a small bias but a much smaller variance than another,unbiased estimator.The concept of "mean square error" estimator combines the two concepts.Let be an estimator of μ.Then the mean square error (MSE)is defined as follows: MSE( )= E( 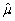- μ)2.Prove that MSE( 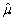)= bias2 + var( 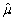).(Hint: subtract and add in E( 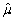)in E( 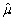- μ)2. )

---

Definitions:

Big-Game Hunting

Big-game hunting involves the tracking and hunting of large animals, often for food, sport, or traditional cultural practices.

Microlith

Small, often pointed stone tools that were part of the toolkit in prehistoric times, used as spear points or arrowheads.

Blade

A thin, flat edge or surface used for cutting or shaping materials, found in tools such as knives, swords, and blades of grass.

Neolithic Transition

The period marking the shift from hunting and gathering communities to agricultural and settlement societies, bringing about significant changes in human lifestyle and culture.