Consider the following model Yt = β0 + 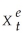 + ut where the superscript "e" indicates expected values.This may represent an example where consumption depends on expected,or "permanent," income.Furthermore,let expected income be formed as follows:
+ ut where the superscript "e" indicates expected values.This may represent an example where consumption depends on expected,or "permanent," income.Furthermore,let expected income be formed as follows: 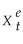 =
= 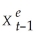 + λ(Xt -
+ λ(Xt - 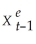 );0 < λ < 1
);0 < λ < 1
(a)In the above expectation formation hypothesis,expectations are formed at the end of the period,say the 31st of December,if you had annual data.Give an intuitive explanation for this process.
(b)Rewrite the expectations equation in the following form: 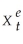 = (1 - λ)
= (1 - λ) 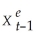 + λXt
+ λXt
Next,following the method used in your textbook,lag both sides of the equation and replace 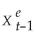 .Repeat this process by repeatedly substituting expression for
.Repeat this process by repeatedly substituting expression for 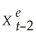 ,
, 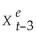 ,and so forth.Show that this results in the following equation:
,and so forth.Show that this results in the following equation: 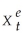 = λXt + λ(1-λ)Xt-1 + λ(1- λ)2 Xt-2 + ...+ λ(1- λ)n Xt-n + (1 - λ)n+1
= λXt + λ(1-λ)Xt-1 + λ(1- λ)2 Xt-2 + ...+ λ(1- λ)n Xt-n + (1 - λ)n+1 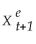 Explain why it is reasonable to drop the last right hand side term as n becomes large.
Explain why it is reasonable to drop the last right hand side term as n becomes large.
(c)Substitute the above expression into the original model that related Y to 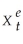 .Although you now have right hand side variables that are all observable,what do you perceive as a potential problem here if you wanted to estimate this distributed lag model without further restrictions?
.Although you now have right hand side variables that are all observable,what do you perceive as a potential problem here if you wanted to estimate this distributed lag model without further restrictions?
(d)Lag both sides of the equation,multiply through by (1- λ),and subtract this equation from the equation found in (c).This is called a "Koyck transformation." What does the resulting equation look like? What is the error process? What is the impact effect (zero-period dynamic multiplier)of a unit change in X,and how does it differ from long run cumulative dynamic multiplier?
Definitions:
Influenza
Also known as the flu, it is a highly contagious viral infection that affects the respiratory system, characterized by fever, chills, muscle aches, cough, and fatigue.
Allergy
An immune system reaction to a foreign substance (allergen) that is not typically harmful to the body.
Surfactant
A fatty molecule on the respiratory membranes.
Alveoli
Tiny air sacs in the lungs where the exchange of oxygen and carbon dioxide takes place.
Q7: Your econometrics textbook stated that there will
Q8: The accompanying graph <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2833/.jpg" alt="The accompanying
Q8: You have collected quarterly data on Canadian
Q23: The random walk model is an example
Q24: Your textbook gave an example of attempting
Q42: (Requires Appendix material)Briefly describe the difference between
Q44: The reason why estimators have a sampling
Q50: Let Y be a random variable.Then var(Y)equals<br>A)
Q58: The slope estimator,β1,has a smaller standard error,other
Q106: A study was performed to examine the