(Requires Appendix Material and Calculus)The Logarithm of the Likelihood Function

question 20

Essay

(Requires Appendix material and Calculus)The logarithm of the likelihood function (L)for estimating the population mean and variance for an i.i.d.normal sample is as follows (note that taking the logarithm of the likelihood function simplifies maximization.It is a monotonic transformation of the likelihood function,meaning that this transformation does not affect the choice of maximum):
L = - 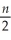log(2πσ2)- 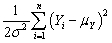Derive the maximum likelihood estimator for the mean and the variance.How do they differ,if at all,from the OLS estimator? Given that the OLS estimators are unbiased,what can you say about the maximum likelihood estimators here? Is the estimator for the variance consistent?

---

Definitions:

Adjusting Entry

A journal entry made at the end of an accounting period to record unbilled, uncollected, or unpaid transactions, ensuring the financial statements are accurate.

Insurance Expense

The cost incurred by a business or individual for obtaining protection against various risks, recorded as an expense in the accounting period in which it is incurred.

Straight-Line Method

A depreciation method in which an asset's cost is evenly spread over its useful life, resulting in equal depreciation charges each period.

Salvage Value

The estimated amount that an asset is worth at the end of its useful life.