You Have a Limited Dependent Variable (Y)and a Single Explanatory

question 41

Essay

You have a limited dependent variable (Y)and a single explanatory variable (X).You estimate the relationship using the linear probability model,a probit regression,and a logit regression.The results are as follows: 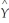= 2.858 - 0.037 × X
(0.007)
Pr(Y = 1 X)= F (15.297 - 0.236 × X)
Pr(Y = 1 X)= Φ (8.900 - 0.137 × X)
(0.058)
(a)Although you cannot compare the coefficients directly,you are told that "it can be shown" that certain relationships between the coefficients of these models hold approximately.These are for the slope: 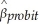≈ 0.625 × , ≈ 0.25 × 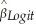.Take the logit result above as a base and calculate the slope coefficients for the linear probability model and the probit regression.Are these values close?
(b)For the intercept,the same conversion holds for the logit-to-probit transformation.However,for the linear probability model,there is a different conversion: 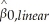≈ 0.2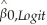5 × + 0.5
Using the logit regression as the base,calculate a few changes in X (temperature in degrees of Fahrenheit)to see how good the approximations are.

---

Definitions:

Resource Pricing

The determination of the price of resources or inputs used in production, based on factors like scarcity, demand, and cost of extraction.

Occupations

Various forms of employment or professions where individuals earn a living by performing specific tasks or services.

Fastest Growing

Referring to entities, such as industries or economies, that experience the most rapid expansion in terms of revenue, size, or influence within a specific period.

Elasticity

An indicator of the degree to which the demand or supply of a product fluctuates following a variation in its price.