Kane Manufacturing Has a Division That Produces Two Models of Grates

question 33

Short Answer

Kane Manufacturing has a division that produces two models of grates, model A and model B. To produce each model A grate requires 3 pounds of cast iron and 6 minutes of labor. To produce each model B grate requires 4 pounds of cast iron and 3 minutes of labor. The profit for each model A grate is $2.00, and the profit for each model B grate is $1.50. Available for grate production each day are 1,160 pounds of cast iron and 22 labor-hours. Because of an excess inventory of model A grates, management has decided to limit the production of model A grates to no more than 180 grates per day.
​
Let x denote the number of model A grates and y the number of model B grates produced. Then, the problem can be reduced to a linear programming problem with the objective function P = 2x + 1.5y and constraints
​ ​
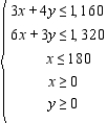
Find the range of values that resource 2 (the constant on the right-hand side of constraint 2) can assume.
​
≤ C _resourse2 ≤
​
By how much can the right-hand side of constraint 3 be decreased so that the current optimal solution still holds?
​
It cannot be decreased by more than __________ units.

---

Definitions:

Economic Elite

A small, relatively exclusive group of people who hold a disproportionate amount of wealth, influence, or power within an economy.

Socially Constructed

Socially constructed refers to the idea that society and culture create and maintain beliefs, behaviors, and norms, rather than these aspects being inherently natural or biological.

Economic Relationships

The interactions and connections between individuals, institutions, and countries regarding the production, distribution, and consumption of goods and services.

Alienation

A state of estrangement or disconnection from others, one's work, or oneself, often resulting in feelings of isolation or disempowerment.