TABLE 14-15 the Superintendent of a School District Wanted to Predict the Predict

question 137

Multiple Choice

TABLE 14-15
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing) , daily average of the percentage of students attending class (% Attendance) , average teacher salary in dollars (Salaries) , and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable, X₁= % Attendance, X₂= Salaries and X₃= Spending:
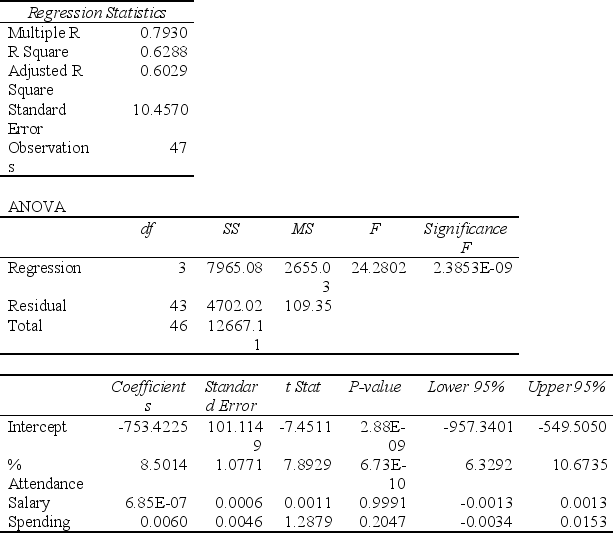Note:

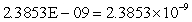
-Referring to Table 14-15, which of the following is the correct alternative hypothesis to determine whether there is a significant relationship between percentage of students passing the proficiency test and the entire set of explanatory variables?

• A) H₁ : β₀ = β₁ = β₂ = β₃ ≠ 0
• B) H₁ : β₁ = β₂ = β₃ ≠ 0
• C) H₁ : At least one of β_j ≠ 0 for j = 0, 1, 2, 3
• D) H₁ : At least one of β_j ≠ 0 for j = 1, 2, 3

Understand the role of personal experiences in shaping personality and self-competency.

Recognize the influence of group memberships on personality development.

Analyze the role of emotional stability in personal and professional settings.

Understand the relationship between various personality traits and success in high-status occupations.

---

Definitions:

Risk Environments

Contexts or situations that contain uncertainties and potential for loss or harm, impacting decision-making processes.

Behavioral Decision Theory

A field of study focusing on the psychology of decision-making processes in individuals and groups.

Complete Certainty

A condition or situation where all relevant information is known and the outcome is guaranteed.

Classical Decision Theory

A theory that focuses on logic and rationality in decision-making processes, often ignoring the influence of emotions and social factors.