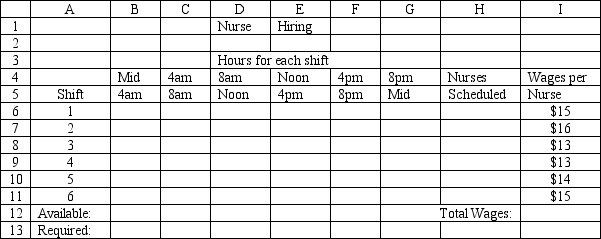
A Hospital Needs to Determine How Many Nurses to Hire

question 22

Essay

A hospital needs to determine how many nurses to hire to cover a 24 hour period. The nurses must work 8 consecutive hours but can start work at the start of 6 different shifts. They are paid different wages depending on when they start their shifts. The number of nurses required per 4-hour time period and their wages are shown in the following table.
$\begin{array}{lcc}\text { Time period } & \text { Required \# of Nurses } & \text { Wage }(\$ / \mathrm{hr}) \\\hline 12 \mathrm{am}-4 \mathrm{am} & 20 & 15 \\4 \mathrm{am}-8 & 30 & 16 \\\text { am } & & \\8 \mathrm{am}-12 \mathrm{pm} & 40 & 13 \\12 \mathrm{pm}-4 \mathrm{pm} & 50 & 13 \\4 \mathrm{pm}-4 & 40 & 14 \\\mathrm{pm}\\8 \mathrm{pm}-12 \mathrm{am}&30 & 15 \end{array}$
What are the key formulas for this Excel spreadsheet implementation of the following formulation?
Let $\quad X _ { i } =$ mumber of nurses warking in thme period $i ; i = 1,6$
$$\begin{array} { l l } \text { MiN: } & 1 \mathbf { X } _ { 1 } + 1 \mathbf { X } _ { \mathbf { 2 } } + 1 \mathbf { X } _ { \mathbf { 3 } } + 1 \mathbf { X } _ { 4 } + 1 \mathbf { X } _ { \mathbf { 5 } } + 1 \mathbf { X } _ { \mathbf { 6 } } \\\text { Subject ta: } & 1 \mathbf { X } _ { 1 } + 1 \mathbf { X } _ { \mathbf { z } } \geq 30 \\& 1 \mathbf { X } _ { \mathbf { 2 } } + 1 \mathbf { X } _ { \mathbf { 3 } } \geq 40 \\& 1 \mathbf { X } _ { \mathbf { 3 } } + 1 \mathbf { X } _ { 4 } \geq 50 \\& 1 \mathbf { X } _ { 4 } + 1 \mathbf { X } _ { \mathbf { 5 } } \geq 40 \\& 1 \mathbf { X } _ { 5 } + 1 \mathbf { X } _ { \mathbf { 1 } } \geq 30 \\& 1 \mathbf { X } _ { 1 } + 1 \mathbf { X } _ { \mathbf { 1 } } \geq 20 \\& \mathbf { X } _ { \mathrm { i } } \geq 0\end{array}$$

---

Definitions:

Probability

The likelihood or chance of an event occurring.

Sample Size

The number of observations or data points that are selected from a population for the purposes of statistical analysis.

Sample Size

The number of observations or data points collected in a sample for the purpose of analysis.

Population Standard Deviation

A measure of the variation or dispersion of all values in an entire population.