TABLE 15-9
Many factors determine the attendance at Major League Baseball games. These factors can include when the game is played, the weather, the opponent, whether or not the team is having a good season, and whether or not a marketing promotion is held. Data from 80 games of the Kansas City Royals for the following variables are collected.
ATTENDANCE = Paid attendance for the game
TEMP = High temperature for the day
WIN% = Team's winning percentage at the time of the game
OPWIN% = Opponent team's winning percentage at the time of the game WEEKEND - 1 if game played on Friday, Saturday or Sunday; 0 otherwise PROMOTION - 1 = if a promotion was held; 0 = if no promotion was held
The regression results using attendance as the dependent variable and the remaining five variables as the independent variables are presented below.
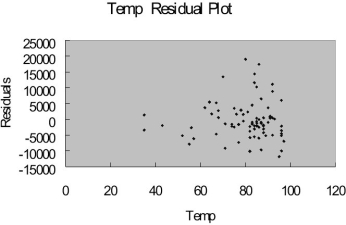
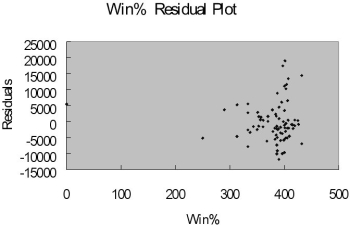
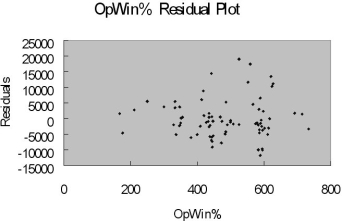
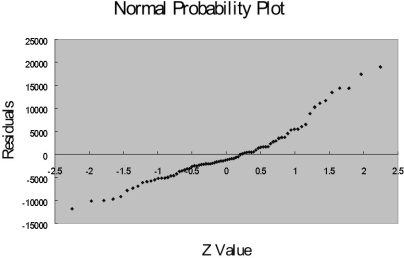
The coefficient of multiple determination ( R 2 j ) of each of the 5 predictors with all the other remaining predictors are,
respectively, 0.2675, 0.3101, 0.1038, 0.7325, and 0.7308.
-Referring to Table 15-9, what is the p-value of the test statistic to determine whether TEMP makes a significant contribution to the regression model in the presence of the other independent variables at a 5% level of significance?
Definitions:
Maintenance Scheduling
The process of planning and organizing maintenance activities in advance, including inspections, repairs, and replacements, to ensure equipment operates efficiently and downtime is minimized.
Prognostic Software Profiles
Software tools that predict the future condition or failure of equipment and systems based on their current and historical operational data.
Spring Pin
A type of fastener used to secure two or more components together, made from sprung (elastic) steel allowing it to compress and then expand for a secure fit.
Zerk Fitting
A grease fitting used to deliver lubricant under pressure into a specific location, commonly found in mechanical systems like automotive suspensions.
Q58: Referring to Table 13-10, 93.98% of the
Q67: Referring to Table 14-3, when the economist
Q87: The manager of a company believed that
Q87: Opportunity loss is the difference between the
Q110: Referring to Table 17-6, what is the
Q142: Referring to Table 13-2, what is the
Q163: The method of least squares is used
Q172: Referring to Table 13-5, the standard error
Q179: Referring to Table 16-14, what are the
Q186: Referring to Table 16-6, a centered 5-year