TABLE 15-9
Many factors determine the attendance at Major League Baseball games. These factors can include when the game is played, the weather, the opponent, whether or not the team is having a good season, and whether or not a marketing promotion is held. Data from 80 games of the Kansas City Royals for the following variables are collected.
ATTENDANCE = Paid attendance for the game
TEMP = High temperature for the day
WIN% = Team's winning percentage at the time of the game
OPWIN% = Opponent team's winning percentage at the time of the game WEEKEND - 1 if game played on Friday, Saturday or Sunday; 0 otherwise PROMOTION - 1 = if a promotion was held; 0 = if no promotion was held
The regression results using attendance as the dependent variable and the remaining five variables as the independent
variables are presented below.
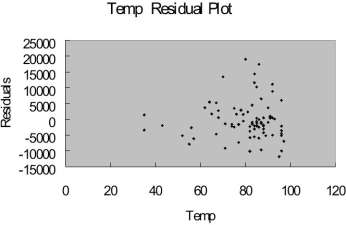
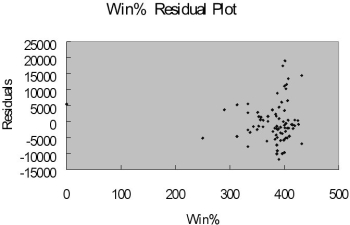
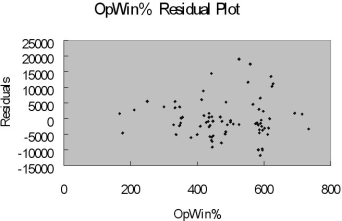
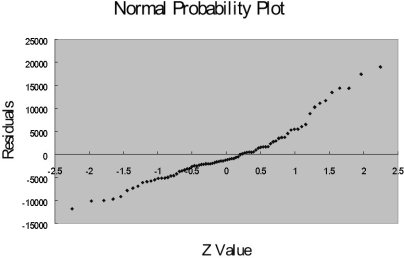
The coefficient of multiple determination ( R 2 j) of each of the 5 predictors with all the other remaining predictors are, respectively, 0.2675, 0.3101, 0.1038, 0.7325, and 0.7308.
-Referring to Table 15-9, there is enough evidence to conclude that TEMP makes a significant contribution to the regression model in the presence of the other independent variables at a 5% level of significance.
Definitions:
Sensory Adaptation
The process by which sensory receptor cells become less sensitive to constant stimuli over time, allowing organisms to focus on changes in their environment.
Sensory Inhibition
The neurological process by which the brain tunes out repetitive, irrelevant stimuli while remaining sensitive to others.
Reaction Formation
A defense mechanism where an individual behaves in a way that is opposite to their own uncomfortable or unacceptable thoughts or feelings.
Paradoxical Heat
A sensation of burning heat felt when a cold stimulus is applied to a specific area of the skin, typically due to nerve damage.
Q2: Referring to Table 18-8, based on the
Q42: Referring to Table 12-2, which test would
Q47: Referring to Table 14-2, for these data,
Q51: In the United States, the control limits
Q58: Referring to Table 16-4 and using a
Q96: Referring to Table 13-12, there is sufficient
Q127: Referring to Table 13-6, which of the
Q137: Referring to Table 14-17, what is the
Q181: Referring to Table 14-6, what are the
Q233: From the coefficient of multiple determination, we