Consider the following two games:
Game 1: There are 10 balls of different colors, you pick one of the proposed balls. After you have made your choice and have put the ball back, one ball is selected at random. If the selected ball matches the ball you picked, you win.
Game 2: There are 6 balls of different colors, you pick two of the proposed balls. After you have made your choices and have put balls back, two different balls are selected at random. If the selected balls match the two you picked, you win.
If you can only play one of these games, which game would you pick to win and why? Use relevant probabilities to justify your choice.
A)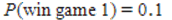 and
and  , therefore it is advantageous to play game 1 because the probability of winning is higher.
, therefore it is advantageous to play game 1 because the probability of winning is higher.
B)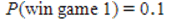 and
and  , therefore it is advantageous to play game 2 because the probability of winning is higher.
, therefore it is advantageous to play game 2 because the probability of winning is higher.
C)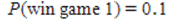 and P(win game 2) = 0.033, therefore it is advantageous to play game 1 because the probability of winning is higher.
and P(win game 2) = 0.033, therefore it is advantageous to play game 1 because the probability of winning is higher.
D)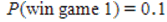 and
and 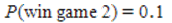 , therefore it is no matter what game to play because the probabilities of winning are equal.
, therefore it is no matter what game to play because the probabilities of winning are equal.
E)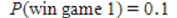 and
and  , therefore it is advantageous to play game 2 because the probability of winning is higher.
, therefore it is advantageous to play game 2 because the probability of winning is higher.
Definitions:
Semi-Fowler's
A semi-upright lying position where the head and torso are raised between 15 and 45 degrees, often used to improve comfort and breathing for patients.
Endotracheal Tube
is a flexible tube inserted through the mouth into the trachea (windpipe) to maintain an open airway, facilitate ventilation, and administer anesthetic gases during surgery.
Mechanical Ventilator
A medical device that provides mechanical breathing support to patients who are unable to breathe adequately on their own.
Auscultate
To listen to the internal sounds of the body, typically using a stethoscope, as part of a medical examination.
Q2: Assuming a random sample from a large
Q5: The mean value of the statistic b
Q8: Consider the following five scatterplots. All are
Q17: A chi-squared goodness-of-fit can be used to
Q32: A hotel chain is interested in evaluating
Q35: Experimental studies utilize blinding to prevent researchers
Q36: Marketing facilitates exchange relationships between buyers and
Q69: As early as 3 years of age,
Q76: Explain how knowledge of marketing enhances consumer
Q105: During the Industrial Revolution demand for manufactured