Solved

The Bigger the Stop Sign, the More Expensive It Is $\operatorname{sqrt}(\cos t)$

question 144

Essay

The bigger the stop sign, the more expensive it is. Here is a graph of the height of a sign in inches versus its cost in dollars.
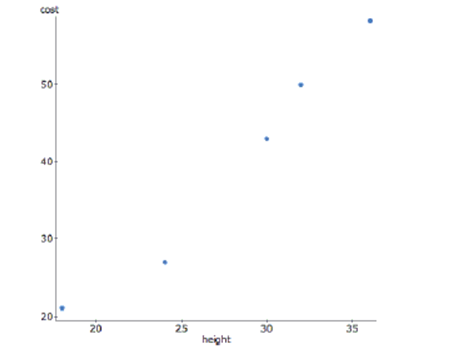
$The bigger the stop sign, the more expensive it is. Here is a graph of the height of a sign in inches versus its cost in dollars. To achieve linearity, the data was transformed using a square root function of cost. Here are the results and a residual plot. Dependent Variable: \operatorname{sqrt}(\cos t) R (correlation coefficient) =0.98946627 R-s q=0.97904349 s: 0.2141 \begin{array}{lrr}\text { Parameter } & \text { coeff } & \text { se } \\ \text { Intercept } & 1.1857 & 0.4346 \\ \text { height } & 0.1792 & 0.0151\end{array} -Interpret R-sq in the context of this problem.$
To achieve linearity, the data was transformed using a square root function of cost. Here are the results and a residual plot.
Dependent Variable: $\operatorname{sqrt}(\cos t)$
$R$ (correlation coefficient) $=0.98946627$
$R-s q=0.97904349$
s: 0.2141
$\begin{array}{lrr}\text { Parameter } & \text { coeff } & \text { se } \\ \text { Intercept } & 1.1857 & 0.4346 \\ \text { height } & 0.1792 & 0.0151\end{array}$

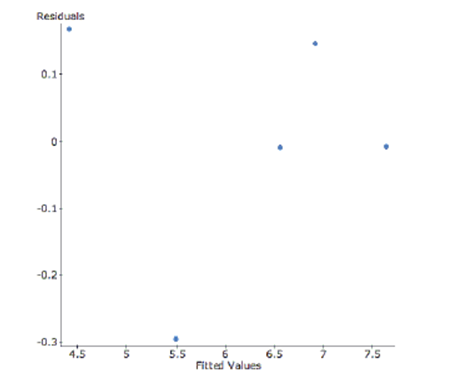
$The bigger the stop sign, the more expensive it is. Here is a graph of the height of a sign in inches versus its cost in dollars. To achieve linearity, the data was transformed using a square root function of cost. Here are the results and a residual plot. Dependent Variable: \operatorname{sqrt}(\cos t) R (correlation coefficient) =0.98946627 R-s q=0.97904349 s: 0.2141 \begin{array}{lrr}\text { Parameter } & \text { coeff } & \text { se } \\ \text { Intercept } & 1.1857 & 0.4346 \\ \text { height } & 0.1792 & 0.0151\end{array} -Interpret R-sq in the context of this problem.$

-Interpret R-sq in the context of this problem.

Definitions:

Testing Process

The series of steps or procedures involved in administering, scoring, and interpreting tests or assessments.

Reliability Improvement

Efforts or methods aimed at increasing the consistency and dependability of a process, instrument, or system.

Client's Stress

The level of psychological strain and pressure experienced by an individual seeking professional help or services.

Reliability Estimates

Statistical measures that indicate the consistency of a test's results over time or across different raters.

The Bigger the Stop Sign, the More Expensive It Is sqrt⁡(cos⁡t) \operatorname{sqrt}(\cos t) sqrt(cost)

Definitions:

The Bigger the Stop Sign, the More Expensive It Is $\operatorname{sqrt}(\cos t)$