Sports Economics Typically Looks at Winning Percentages of Sports Teams

question 5

Essay

Sports economics typically looks at winning percentages of sports teams as one of various outputs, and estimates production functions by analyzing the relationship between the winning percentage and inputs. In Major League Baseball (MLB), the determinants of winning are quality pitching and batting. All 30 MLB teams for the 1999 season. Pitching quality is approximated by "Team Earned Run Average" (ERA), and hitting quality by "On Base Plus Slugging Percentage" (OPS).
Summary of the Distribution of Winning Percentage, On Base Plus Slugging Percentage,
and Team Earned Run Average for MLB in 1999 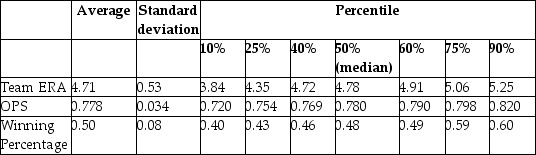Your regression output is:
$$\begin{array} { l } \widehat { \text { Winpct } } = - 0.19 - 0.099 \times \text { teamera } + 1.490 \times \text { ops, } R 2 = 0.92 , \text { SER } = 0.02 \text {. } \\\quad\quad\quad\quad\quad\text { (0.08) (0.008) }\quad\quad\quad\quad\quad\quad(0.126) \\\end{array}$$
(a)Interpret the regression. Are the results statistically significant and important?
(b)There are two leagues in MLB, the American League (AL)and the National League (NL). One major difference is that the pitcher in the AL does not have to bat. Instead there is a "designated hitter" in the hitting line-up. You are concerned that, as a result, there is a different effect of pitching and hitting in the AL from the NL. To test this hypothesis, you allow the AL regression to have a different intercept and different slopes from the NL regression. You therefore create a binary variable for the American League (DAL)and estimate the following specification: $\begin{aligned}\widehat { \text { Winpct } = - } & 0.29 + 0.10 \times D A L - 0.100 \times \text { teamera } + 0.008 \times ( \text { DAL } \times \text { teamera } ) \\& ( 0.12 ) ( 0.24 ) \quad\quad\quad\quad ( 0.008 )\quad\quad\quad\quad(0.018) \\\\& + 1.622 ^ { * } \text { ops } - 0.187 ^ { * } ( D A L \times \text { ops } ) , R 2 = 0.92 , S E R = 0.02 . \\& ( 0.163 ) \quad\quad\quad\quad ( 0.160 )\end{aligned}$
What is the regression for winning percentage in the AL and NL? Next, calculate the t-statistics and say something about the statistical significance of the AL variables. Since you have allowed all slopes and the intercept to vary between the two leagues, what would the results imply if all coefficients involving DAL were statistically significant?
(c)You remember that sequentially testing the significance of slope coefficients is not the same as testing for their significance simultaneously. Hence you ask your regression package to calculate the F-statistic that all three coefficients involving the binary variable for the AL are zero. Your regression package gives a value of 0.35. Looking at the critical value from you F-table, can you reject the null hypothesis at the 1% level? Should you worry about the small sample size?

Identify the roles and benefits of outsourcing HR functions and the types of activities that can be outsourced.

Distinguish between strategic, analytic, and transactional HR operations in the context of information technology applications.

Analyze the impact of web-based HR processes, such as online recruiting and e-learning.

Comprehend the significance and usage of workforce analytics and big data in HR decision-making.

---

Definitions:

Nasopharynx

The upper part of the throat that lies behind the nose and above the soft palate, serving as a passageway for air from the nose to the throat and lungs.

Laryngopharynx

The region of the throat that connects the oropharynx above with the trachea and esophagus below, facilitating the passage of food and air.

Catabolism

The breakdown of complex molecules in living organisms to form simpler ones, often releasing energy.

Complex Substances

Materials composed of two or more chemical elements or compounds, having intricate and multifaceted structures.