To Examine the Differences Between Salaries of Male and Female

question 1

Multiple Choice

To examine the differences between salaries of male and female middle managers of a large bank, 90 individuals were randomly selected, and two models were created with the following variables considered: Salary = the monthly salary (excluding fringe benefits and bonuses) ,
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual; 1 for males, and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
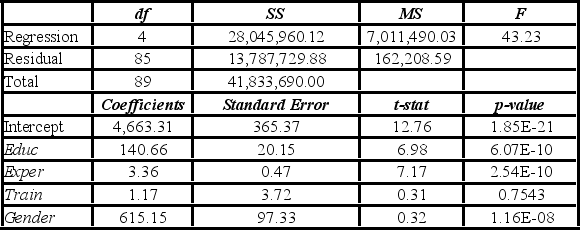
Model A: Salary = β₀ + β₁Educ + β₂Exper + β₃Train + β₄Gender + ε Model B: Salary = β₀ + β₁Educ + β₂Exper + β₃Gender + ε 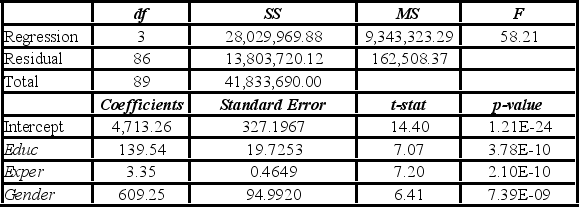The variable Train is deleted from Model A which results in Model B. Which of the following justifies this choice?

• A) The adjusted R² Model B is lower than the adjusted R² of Model A, and the variable is individually significant in Model A.
• B) The adjusted R² of Model B is higher than the adjusted R² of Model A, and the variable is individually significant in Model A.
• C) The adjusted R² of Model B is lower than the adjusted R² of Model A, and the variable is not individually significant in Model A.
• D) The adjusted R² of Model B is higher than the adjusted R² of Model A, and the variable is not individually significant in Model A.

---

Definitions:

Specific Identification

An inventory costing method that tracks the exact cost of each individual item in inventory to determine cost of goods sold.

Estimated Gross Profit

An expected amount of profit calculated by subtracting the estimated cost of goods sold from the estimated total sales revenue.

Sales Totaled

This term refers to the aggregate amount of revenue generated from the sale of goods or services over a specific period.

Inventory Cost

The total cost incurred for obtaining, storing, and managing inventory that has not yet been sold.