Instruction 12 $\text { Regression statistics }$ $\text { ANOVA }$

question 57

Short Answer

Instruction 12.35
A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware. Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed:
$\text { Regression statistics }$
$\begin{array}{|l|l|}\hline \text { MultipleR } & 0.8691 \\\hline \text { R Square } & 0.7554 \\\hline \begin{array}{l}\text { Adjusted R } \\\text { Square }\end{array} & 0.7467 \\\hline \text { Standard Error } & 44.4765 \\\hline \text { Observations } & 30.0000\\\hline \end{array}$

$\text { ANOVA }$
$\begin{array}{|l|l|l|l|l|l|}\hline & d f & S S & M S & F & \begin{array}{l}\text { Significance } \\F\end{array} \\\hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\\hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\\hline \text { Total } & 29 & 226451.3503 & & & \\\hline\end{array}$

$\begin{array}{|l|l|l|l|l|l|l|}\hline & \text { Coefficients } & \begin{array}{l}\text { Standard } \\\text { Error }\end{array} & \text { t Stat } & p \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\\hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \\\hline\end{array}$



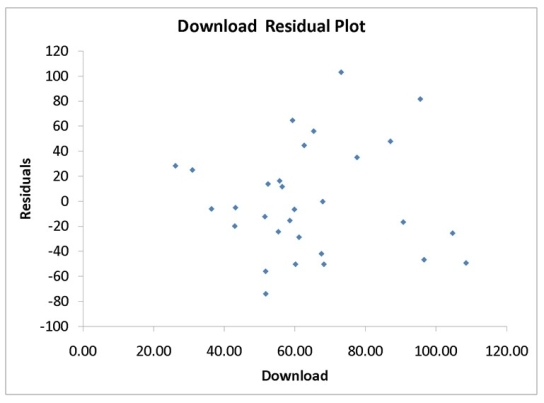
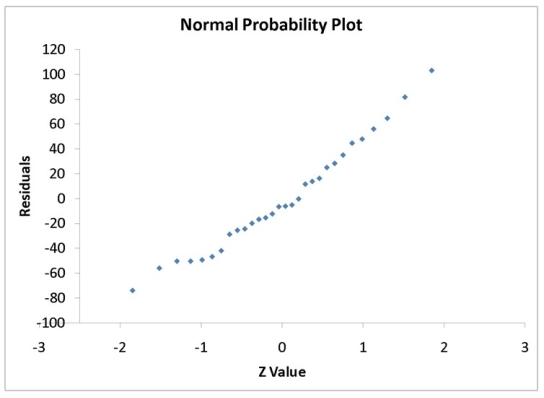
-Referring to Instruction 12.35,what are the lower and upper limits of the 95% confidence interval estimate for the mean change in revenue as a result of a 1 thousand increase in the number of downloads?

---

Definitions:

Four Corners

The term usually relates to the geographical region in the southwestern United States where the states of Arizona, New Mexico, Utah, and Colorado meet at a single point. In a legal document context, it refers to the principle that the interpretation of the document is derived from what is within its "four corners," meaning its explicit content, without reference to external factors.

Void Contract

A legal agreement that is invalid or unenforceable from the outset.

Illegal Drugs

Substances whose production, sale, or possession is prohibited by law due to their potential for abuse and harm.

Smuggle

The act of illegally transporting goods or people across borders, typically to avoid taxes or regulations.