Let p be the success probability of a Bernoulli random variable Y,i.e. ,p = Pr(Y = 1).It can be shown that 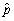 ,the fraction of successes in a sample,is asymptotically distributed N(p,
,the fraction of successes in a sample,is asymptotically distributed N(p, 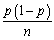 .Using the estimator of the variance of
.Using the estimator of the variance of 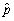 ,
, 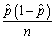 ,construct a 95% confidence interval for p.Show that the margin for sampling error simplifies to 1/
,construct a 95% confidence interval for p.Show that the margin for sampling error simplifies to 1/ 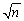 if you used 2 instead of 1.96 assuming,conservatively,that the standard error is at its maximum.Construct a table indicating the sample size needed to generate a margin of sampling error of 1%,2%,5% and 10%.What do you notice about the increase in sample size needed to halve the margin of error? (The margin of sampling error is 1.96×SE(
if you used 2 instead of 1.96 assuming,conservatively,that the standard error is at its maximum.Construct a table indicating the sample size needed to generate a margin of sampling error of 1%,2%,5% and 10%.What do you notice about the increase in sample size needed to halve the margin of error? (The margin of sampling error is 1.96×SE( 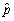 ))
))
Definitions:
Mirror Examination
The practice of investigating one's own body using a mirror to promote body positivity and self-awareness.
Homework Exercises
Tasks assigned by educators to be completed outside of class to reinforce learning and assess student understanding.
Sexual Anxieties
Feelings of fear, worry, or unease regarding sexual activities, performance, or desirability.
Sexual Abuse
Any form of non-consensual sexual contact or behavior towards an individual, ranging from harassment to assault, often resulting in psychological trauma.
Q8: An extension of the Solow growth model
Q9: One of the properties of the OLS
Q14: Consider the following model<br>Yt = α0 +
Q16: You have decided to analyze the year-to-year
Q20: Consider the following earnings function:<br>ahei= β0 +
Q21: Females,it is said,make 70 cents to the
Q26: Lower transaction costs are one advantage of
Q33: A foreign currency long hedge with a
Q48: To prove that the OLS estimator is
Q62: Using a spreadsheet program such as Excel,plot